题目内容
已知直线l:y=x+m与抛物线y2=8x交于A、B两点,
(1)若|AB|=10,求m的值;
(2)若OA⊥OB,求m的值.
(1)若|AB|=10,求m的值;
(2)若OA⊥OB,求m的值.
设A(x1,y1)、B(x2,y2)
(1)
⇒x2+(2m-8)x+m2=0------------------------------(1分)
⇒
-----------------------------------------------(3分)|AB|=
|x1-x2|=
=10,m=
----(5分)
∵m<2,∴m=
---------------------------------------------------------(6分)
(2)∵OA⊥OB,∴x1x2+y1y2=0------------------------------------(7分)
x1x2+(x1+m)(x2+m)=0,2x1x2+m(x1+x2)+m2=0-----------------------------------------(9分)
2m2+m(8-2m)+m2=0,m2+8m=0,m=0orm=-8,---------------------------------(11分)
经检验m=-8------------------------------------------------------------(12分)
(1)
|
⇒
|
| 2 |
| 2 |
| (x1+x2)2-4x1x2 |
| 7 |
| 16 |
∵m<2,∴m=
| 7 |
| 16 |
(2)∵OA⊥OB,∴x1x2+y1y2=0------------------------------------(7分)
x1x2+(x1+m)(x2+m)=0,2x1x2+m(x1+x2)+m2=0-----------------------------------------(9分)
2m2+m(8-2m)+m2=0,m2+8m=0,m=0orm=-8,---------------------------------(11分)
经检验m=-8------------------------------------------------------------(12分)

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
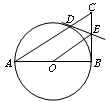
 的直径
的直径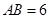 ,
,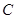 为圆周上一点,
为圆周上一点,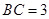 .过
.过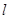 ,过
,过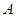 作
作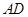 ,
, 、
、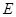 ,则线段
,则线段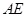 的长为 .
的长为 .