题目内容
P(x0,y0)(x0≠±a)是双曲线E:
-
=1(a>0,b>0)上一点,M,N分别是双曲线E的左右顶点,直线PM,PN的斜率之积为
.
(1)求双曲线的离心率;
(2)过双曲线E的右焦点且斜率为1的直线交双曲线于A,B两点,O为坐标原点,C为双曲线上一点,满足
=λ
+
,求λ的值.
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 5 |
(1)求双曲线的离心率;
(2)过双曲线E的右焦点且斜率为1的直线交双曲线于A,B两点,O为坐标原点,C为双曲线上一点,满足
| OC |
| OA |
| OB |
(1)∵P(x0,y0)(x0≠±a)是双曲线E:
-
=1(a>0,b>0)上一点,
∴
-
=1,
由题意又有
•
=
,
可得a2=5b2,c2=a2+b2,
则e=
=
,
(2)联立
,得4x2-10cx+35b2=0,
设A(x1,y1),B(x2,y2),
则x1+x2=
,x1•x2=
,
设
=(x3,y3),
=λ
+
,
即
又C为双曲线上一点,即x32-5y32=5b2,
有(λx1+x2)2-5(λy1+y2)2=5b2,
化简得:λ2(x12-5y12)+(x22-5y22)+2λ(x1x2-5y1y2)=5b2,
又A(x1,y1),B(x2,y2)在双曲线上,所以x12-5y12=5b2,x22-5y22=5b2,
而x1x2-5y1y2=x1x2-5(x1-c)(x2-c)=-4x1x2+5c(x1+x2)-5c2=10b2,
得λ2+4λ=0,解得λ=0或-4.
| x2 |
| a2 |
| y2 |
| b2 |
∴
| x02 |
| a2 |
| y02 |
| b2 |
由题意又有
| y0 |
| x0-a |
| y0 |
| x0+a |
| 1 |
| 5 |
可得a2=5b2,c2=a2+b2,
则e=
| c |
| a |
| ||
| 5 |
(2)联立
|
设A(x1,y1),B(x2,y2),
则x1+x2=
| 5c |
| 2 |
| 35b2 |
| 4 |
设
| OC |
| OC |
| OA |
| OB |
即
|
又C为双曲线上一点,即x32-5y32=5b2,
有(λx1+x2)2-5(λy1+y2)2=5b2,
化简得:λ2(x12-5y12)+(x22-5y22)+2λ(x1x2-5y1y2)=5b2,
又A(x1,y1),B(x2,y2)在双曲线上,所以x12-5y12=5b2,x22-5y22=5b2,
而x1x2-5y1y2=x1x2-5(x1-c)(x2-c)=-4x1x2+5c(x1+x2)-5c2=10b2,
得λ2+4λ=0,解得λ=0或-4.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目

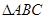 是圆的内接三角行,
是圆的内接三角行,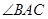 的平分线交圆于点D,交BC于E,过点B的圆的切线与AD的延长线交于点F,在上述条件下,给出下列四个结论:①BD平分
的平分线交圆于点D,交BC于E,过点B的圆的切线与AD的延长线交于点F,在上述条件下,给出下列四个结论:①BD平分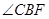 ;②
;②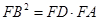 ;③
;③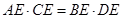 ;④
;④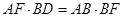 .则所有正确结论的序号是( )
.则所有正确结论的序号是( )