题目内容
椭圆C:
+
=1(a>b>0),点A为左顶点,点B为上顶点,直线AB的斜率为
,又直线y=k(x-1)经过椭圆C的一个焦点且与其相交于点M,N.
(Ⅰ)求椭圆C的方程;
(Ⅱ)将|MN|表示为k的函数;
(Ⅲ)线段MN的垂直平分线与x轴相交于点P,又点Q(1,0),求证:
为定值.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)将|MN|表示为k的函数;
(Ⅲ)线段MN的垂直平分线与x轴相交于点P,又点Q(1,0),求证:
| |PQ| |
| |MN| |
(Ⅰ)如图,
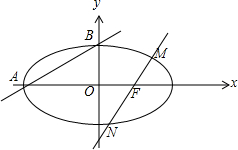
∵直线AB的斜率为
,
∴
=
,
又直线y=k(x-1)经过椭圆C的一个焦点,
∴交点F(1,0).
则
,解得a2=4,b2=3.
∴椭圆C的方程为
+
=1;
(Ⅱ)联立
,得(3+4k2)x2-8k2x+4k2-12=0.
设M(x1,y1),N(x2,y2),
则x1+x2=
,x1x2=
.
∴|MN|=
=
=
.
(Ⅲ)证明:线段MN的中点的横坐标为
=
,纵坐标为k•(
-1)=
.
∴线段MN的垂直平分线方程为y+
=k(x-
),
取y=0,得x=
,
∴P(
,0),
则|PQ|=1-
=
.
则
=
=
为定值.

∵直线AB的斜率为
| ||
| 2 |
∴
| b |
| a |
| ||
| 2 |
又直线y=k(x-1)经过椭圆C的一个焦点,
∴交点F(1,0).
则
|
∴椭圆C的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)联立
|
设M(x1,y1),N(x2,y2),
则x1+x2=
| 8k2 |
| 3+4k2 |
| 4k2-12 |
| 3+4k2 |
∴|MN|=
| 1+k2 |
| (x1+x2)2-4x1x2 |
=
| 1+k2 |
(
|
| 12(1+k2) |
| 3+4k2 |
(Ⅲ)证明:线段MN的中点的横坐标为
| x1+x2 |
| 2 |
| 4k2 |
| 3+4k2 |
| 4k2 |
| 3+4k2 |
| -3k |
| 3+4k2 |
∴线段MN的垂直平分线方程为y+
| 3k |
| 3+4k2 |
| 4k2 |
| 3+4k2 |
取y=0,得x=
| k2 |
| 3+4k2 |
∴P(
| k2 |
| 3+4k2 |
则|PQ|=1-
| k2 |
| 3+4k2 |
| 3(1+k2) |
| 3+4k2 |
则
| |PQ| |
| |MN| |
| ||
|
| 1 |
| 4 |

练习册系列答案
相关题目
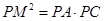 ;
;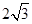 ,OA=
,OA=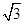 OM,求MN的长.
OM,求MN的长.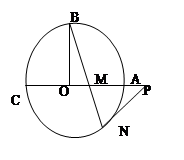
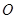 ,BD是圆
,BD是圆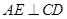 于点E,DA平分
于点E,DA平分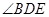 .
.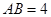 ,
,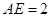 ,求CD.
,求CD.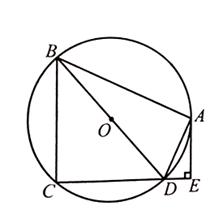
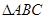 是圆的内接三角行,
是圆的内接三角行,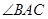 的平分线交圆于点D,交BC于E,过点B的圆的切线与AD的延长线交于点F,在上述条件下,给出下列四个结论:①BD平分
的平分线交圆于点D,交BC于E,过点B的圆的切线与AD的延长线交于点F,在上述条件下,给出下列四个结论:①BD平分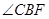 ;②
;②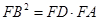 ;③
;③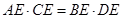 ;④
;④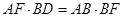 .则所有正确结论的序号是( )
.则所有正确结论的序号是( )