题目内容
已知抛物线C:y2=8x与点M(-2,2),过C的焦点且斜率为k的直线与C交于A、B两点,若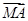 ·
·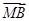 =0,则k等于( )
=0,则k等于( )
(A)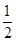 (B)
(B)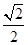 (C)
(C) 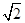 (D)2
(D)2
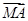 ·
·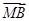 =0,则k等于( )
=0,则k等于( )(A)
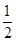 (B)
(B)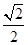 (C)
(C) 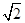 (D)2
(D)2D
法一 设直线方程为y=k(x-2),A(x1,y1)、B(x2,y2),
由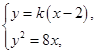
得k2x2-4(k2+2)x+4k2=0,
∴x1+x2=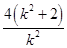 ,
,
x1x2=4,
由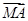 ·
·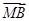 =0,
=0,
得(x1+2,y1-2)·(x2+2,y2-2)=(x1+2)(x2+2)+[k(x1-2)-2][k(x2-2)-2]=0,
代入整理得k2-4k+4=0,
解得k=2.故选D.
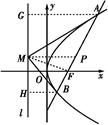
法二 如图所示,设F为焦点,取AB中点P,
过A、B分别作准线的垂线,垂足分别为G、H,
连接MF,MP,
由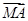 ·
·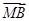 =0,
=0,
知MA⊥MB,
则|MP|=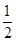 |AB|=
|AB|=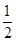 (|AG|+|BH|),
(|AG|+|BH|),
所以MP为直角梯形BHGA的中位线,
所以MP∥AG∥BH,
所以∠GAM=∠AMP=∠MAP,
又|AG|=|AF|,
|AM|=|AM|,
所以△AMG≌△AMF,
所以∠AFM=∠AGM=90°,
则MF⊥AB,所以k=-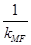 =2.
=2.
由
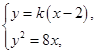
得k2x2-4(k2+2)x+4k2=0,
∴x1+x2=
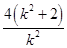 ,
,x1x2=4,
由
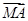 ·
·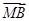 =0,
=0,得(x1+2,y1-2)·(x2+2,y2-2)=(x1+2)(x2+2)+[k(x1-2)-2][k(x2-2)-2]=0,
代入整理得k2-4k+4=0,
解得k=2.故选D.
法二 如图所示,设F为焦点,取AB中点P,
过A、B分别作准线的垂线,垂足分别为G、H,
连接MF,MP,

由
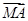 ·
·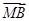 =0,
=0,知MA⊥MB,
则|MP|=
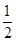 |AB|=
|AB|=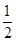 (|AG|+|BH|),
(|AG|+|BH|),所以MP为直角梯形BHGA的中位线,
所以MP∥AG∥BH,
所以∠GAM=∠AMP=∠MAP,
又|AG|=|AF|,
|AM|=|AM|,
所以△AMG≌△AMF,
所以∠AFM=∠AGM=90°,
则MF⊥AB,所以k=-
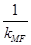 =2.
=2.
练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
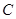 在
在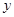 轴右侧,
轴右侧, 的距离减去它到
的距离减去它到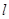 交曲线
交曲线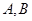 两点,线段
两点,线段 的中点为
的中点为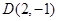 ,求直线
,求直线 的焦点F作直线AB,CD与抛物线交于A、B、C、D四点,且
的焦点F作直线AB,CD与抛物线交于A、B、C、D四点,且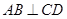 ,则
,则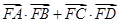 的最大等于 ( )
的最大等于 ( )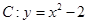 ,过原点的动直线
,过原点的动直线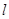 交抛物线
交抛物线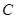 于
于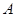 、
、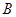 两点,
两点,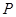 是
是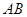 的中点,设动点
的中点,设动点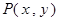 ,则
,则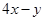 的最大值是( )
的最大值是( )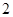
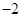
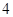
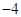
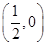 的距离比到y轴的距离大
的距离比到y轴的距离大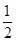 .记点P的轨迹为曲线C.
.记点P的轨迹为曲线C.