题目内容
已知P,Q为抛物线x2=2y上两点,点P,Q的横坐标分别为4,-2,过P,Q分别作抛物线的切线,两切线交于点A,则点A的纵坐标为( )
| A.1 | B.3 | C.-4 | D.-8 |
C
y=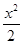 ,y′=x,
,y′=x,
∴y′|x=4=4,y′|x=-2=-2,
点P的坐标为(4,8),点Q的坐标为(-2,2),
∴在点P处的切线方程为y-8=4(x-4),
即y=4x-8.
在点Q处的切线方程为y-2=-2(x+2),
即y=-2x-2,解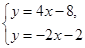 得A(1,-4),则A点的纵坐标为-4.
得A(1,-4),则A点的纵坐标为-4.
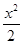 ,y′=x,
,y′=x,∴y′|x=4=4,y′|x=-2=-2,
点P的坐标为(4,8),点Q的坐标为(-2,2),
∴在点P处的切线方程为y-8=4(x-4),
即y=4x-8.
在点Q处的切线方程为y-2=-2(x+2),
即y=-2x-2,解
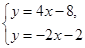 得A(1,-4),则A点的纵坐标为-4.
得A(1,-4),则A点的纵坐标为-4.
练习册系列答案
相关题目
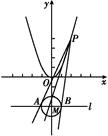
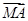 ·
·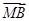 =0,则k等于( )
=0,则k等于( )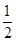 (B)
(B)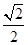 (C)
(C) 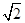 (D)2
(D)2 x2+2上一动点P(x,y),则y+|PQ|最小值为( )
x2+2上一动点P(x,y),则y+|PQ|最小值为( )