题目内容
直线y=x-3与抛物线y2=4x交于A,B两点,过A,B两点向抛物线的准线作垂线,垂足分别为P,Q,则梯形APQB的面积为( )
| A.48 | B.56 | C.64 | D.72 |
A
由题不妨设A在第一象限,联立y=x-3和y2=4x可
得A(9,6),B(1,-2),而准线方程是
x=-1,所以AP=10,QB=2,PQ=8,
故S梯形APQB= (AP+QB)·PQ=48.
(AP+QB)·PQ=48.
得A(9,6),B(1,-2),而准线方程是
x=-1,所以AP=10,QB=2,PQ=8,
故S梯形APQB=
 (AP+QB)·PQ=48.
(AP+QB)·PQ=48.
练习册系列答案
相关题目
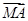 ·
·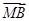 =0,则k等于( )
=0,则k等于( )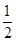 (B)
(B)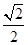 (C)
(C) 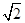 (D)2
(D)2 x2+2上一动点P(x,y),则y+|PQ|最小值为( )
x2+2上一动点P(x,y),则y+|PQ|最小值为( )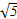
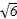
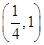 ,那么点A到此抛物线的焦点的距离为________.
,那么点A到此抛物线的焦点的距离为________.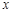 轴垂直,且经过点
轴垂直,且经过点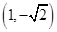 的抛物线方程是( )
的抛物线方程是( )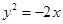
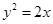
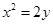
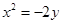
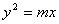 的准线与直线
的准线与直线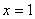 之间的距离为3,则该抛物线的方程为 .
之间的距离为3,则该抛物线的方程为 .