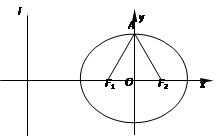题目内容
(12分)已知抛物线 :
: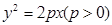 过点
过点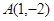 .(1)求抛物线
.(1)求抛物线 的方程,并求其准线方程;
的方程,并求其准线方程;
(2)是否存在平行于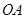 (
( 为坐标原点)的直线
为坐标原点)的直线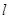 ,使得直线
,使得直线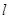 与抛物线
与抛物线 有公共点,且直线
有公共点,且直线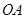 与
与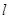 的
的
距离等于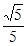 ?若存在,求出直线
?若存在,求出直线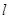 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
(1)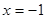 . (2)符合题意的直线存在,其方程为
. (2)符合题意的直线存在,其方程为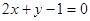 .
.
解析试题分析:(1)将点(1,-2)代入抛物线方程可求出p值,从而得到抛物线的方程,进而得到其准线方程.
(2) 假设存在符合题意的直线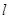 ,其方程为
,其方程为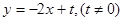 ,由于直线l与抛物线C有公共点,所以它与抛物线方程联立消去x后得到关于y的一元二次方程的判断式
,由于直线l与抛物线C有公共点,所以它与抛物线方程联立消去x后得到关于y的一元二次方程的判断式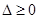 ,从而解得
,从而解得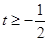 .
.
然后再利用平行线间的距离公式得到t的方程求出t值,看是否满足t的范围,从而确定是否存在这样的直线.
(1)将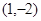 代入
代入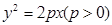 ,得
,得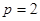 ,故所求的抛物线
,故所求的抛物线 的标准方程为
的标准方程为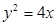 .
.
其准线方程为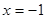 . ……… 4分
. ……… 4分
(2)假设存在符合题意的直线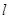 ,其方程为
,其方程为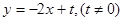 .由
.由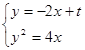 ,得
,得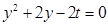 .
.
因为直线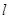 与抛物线
与抛物线 有公共点,所以
有公共点,所以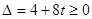 ,解得
,解得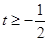 .另一方面,由直线
.另一方面,由直线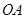 与
与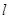 的距
的距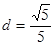 可得
可得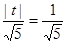 ,解得
,解得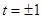 .又因为
.又因为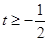 ,
,
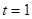 ,所以符合题意的直线存在,其方程为
,所以符合题意的直线存在,其方程为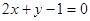 .…12分
.…12分
考点:抛物线的标准方程,直线与抛物线的位置关系,平行线间的距离公式.
点评:直线与抛物线的位置关系的判定可由它们的方程联立消去一个变量后得到另一个变量的二次方程,再通过判别式进行判断即可.但要注意二次项系数是否为零的问题.

练习册系列答案
相关题目
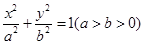 的上顶点为A,左顶点为B, F为右焦点, 过F作平行于AB的直线交椭圆于C、D两点. 作平行四边形OCED, E恰在椭圆上。
的上顶点为A,左顶点为B, F为右焦点, 过F作平行于AB的直线交椭圆于C、D两点. 作平行四边形OCED, E恰在椭圆上。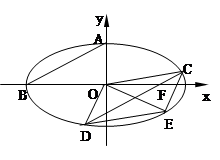
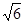 , 求椭圆的方程.
, 求椭圆的方程.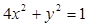 及直线
及直线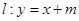 ,当直线和椭圆有公共点时.
,当直线和椭圆有公共点时.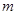 的取值范围;
的取值范围;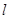 的方程.
的方程.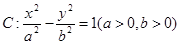 的离心率为
的离心率为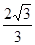 ,且过点P(
,且过点P(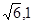 ).
).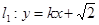 与双曲线C恒有两个不同的交点A,B,且
与双曲线C恒有两个不同的交点A,B,且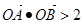
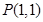 为椭圆
为椭圆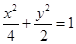 内的一定点,过P点引一直线,与椭圆相交于
内的一定点,过P点引一直线,与椭圆相交于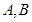 两点,且P恰好为弦AB的中点,如图所示,求弦AB所在的直线方程及弦AB的长度。
两点,且P恰好为弦AB的中点,如图所示,求弦AB所在的直线方程及弦AB的长度。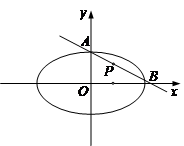
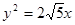 的焦点是双曲线C的一个焦点,且双曲线经过点
的焦点是双曲线C的一个焦点,且双曲线经过点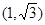 ,又知直线
,又知直线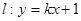 与双曲线C相交于A、B两点.
与双曲线C相交于A、B两点.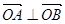 ,求实数k值.
,求实数k值.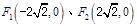 ,长轴长为6,
,长轴长为6,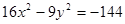 的焦点坐标,离心率和渐近线方程.
的焦点坐标,离心率和渐近线方程.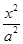 +
+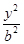 =1(a>b>0)的焦点F1,F2和短轴的一个端点A构成等边三角形,
=1(a>b>0)的焦点F1,F2和短轴的一个端点A构成等边三角形,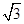 ,
,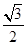 )在椭圆C上,直线l为椭圆C的左准线.
)在椭圆C上,直线l为椭圆C的左准线.