题目内容
已知双曲线C的中心在原点,抛物线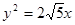 的焦点是双曲线C的一个焦点,且双曲线经过点
的焦点是双曲线C的一个焦点,且双曲线经过点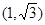 ,又知直线
,又知直线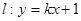 与双曲线C相交于A、B两点.
与双曲线C相交于A、B两点.
(1)求双曲线C的方程;
(2)若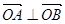 ,求实数k值.
,求实数k值.
(1)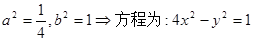 ;(2)
;(2)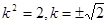 ,检验合格.
,检验合格.
解析试题分析:(1)根据抛物线的方程求出焦点坐标得到c 值,再根据双曲线过点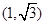 可建立关于a,b的方程,求出a,b的值,从而得到双曲线的方程.
可建立关于a,b的方程,求出a,b的值,从而得到双曲线的方程.
(2)设直线方程为y=kx+1,
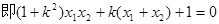
所以直线方程与双曲线方程联立消去y得到关于x的一元二次方程,求出两个根和,两个积代入上式可建立关于k的方程求出k的值.
(1)抛物线的焦点是(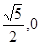 ),则双曲线的
),则双曲线的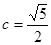 .………………1分
.………………1分
设双曲线方程: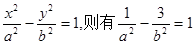 …………………………2分
…………………………2分
解得: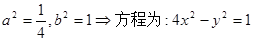 …………………………5分
…………………………5分
(2)联立方程: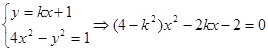
当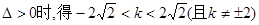 ……………………7分(未写△扣1分)
……………………7分(未写△扣1分)
由韦达定理: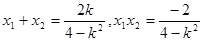 ……………………8分
……………………8分
设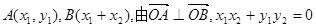
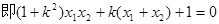 代入可得:
代入可得: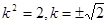 ,检验合格.……12分.
,检验合格.……12分.
考点:双曲线与抛物线的标准方程及其性质,直线与双曲线的位置关系.
点评:在求双曲线的标准方程时要注意焦点位置,直线与双曲线的位置关系的问题一般要通过方程联立,借助韦达定理和判别式解决.

练习册系列答案
相关题目
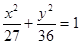 有相同焦点,且经过点
有相同焦点,且经过点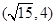 ,
,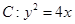 ,
, 是抛物线
是抛物线 的焦点,过点
的焦点,过点 与
与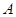 、
、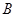 两点,
两点,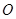 为坐标原点.
为坐标原点. 为直径的圆的方程;
为直径的圆的方程;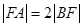 ,求直线
,求直线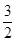 ),两个焦点为(-1,0)(1,0)?
),两个焦点为(-1,0)(1,0)? :
: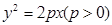 过点
过点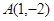 .(1)求抛物线
.(1)求抛物线 (
( 为坐标原点)的直线
为坐标原点)的直线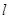 ,使得直线
,使得直线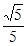 ?若存在,求出直线
?若存在,求出直线
 的坐标为
的坐标为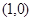 ;
;
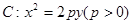 和点
和点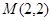 ,.斜率为
,.斜率为 的直线与抛物线
的直线与抛物线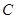 相交不同的两个点
相交不同的两个点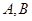 .若点
.若点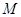 恰好为
恰好为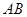 的中点.
的中点.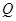 ,使得经过点
,使得经过点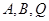 的圆和抛物线
的圆和抛物线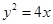 的焦点为
的焦点为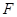 ,过点
,过点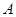 ,
, 两点.
两点.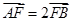 ,求直线
,求直线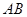 的斜率;
的斜率;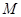 在线段
在线段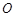 关于点
关于点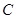 ,求四边形
,求四边形 面积的最小值.
面积的最小值.