Question

【题目】已知x∈（0， ），则函数f（x）=sinxtanx+cosxcotx的值域为（ ）
A.[1，2）
B.[ ，+∞）
C.（1， ]
D.[1，+∞）

Answer 1

【答案】B
【解析】解：x∈（0， ）时，
函数f（x）=sinxtanx+cosxcotx
= +
=
=
= ；
令sinx+cosx=t，
则t= sin（x+ ），sinxcosx= ；
∵x∈（0， ），
∴sin（x+ ）∈（ ，1]，t∈（1， ]；
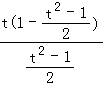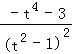∴f（x）可化为f（t）= = ，∴f′（t）= ＜0，
∴t∈（1， ]时，函数f（t）是单调减函数；
当t= 时，函数f（t）取得最小值f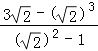（ ）= = ，且无最大值；
∴函数f（x）的值域是[ ，+∞）．
故选：B．
【考点精析】认真审题，首先需要了解三角函数的最值(函数，当时，取得最小值为；当时，取得最大值为，则，，)．