题目内容
已知经过椭圆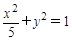 的焦点且与其对称轴成
的焦点且与其对称轴成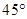 的直线与椭圆交于
的直线与椭圆交于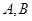 两点,
两点,
则|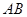 |=( ).
|=( ).
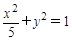 的焦点且与其对称轴成
的焦点且与其对称轴成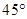 的直线与椭圆交于
的直线与椭圆交于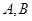 两点,
两点,则|
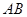 |=( ).
|=( ).A.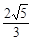 | B. | C.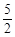 | D.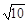 |
A
试题分析:椭圆
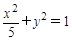 的焦点为
的焦点为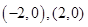 ,不妨设直线过点
,不妨设直线过点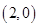 ,因为直线斜率为
,因为直线斜率为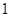 ,所以直线方程为:
,所以直线方程为: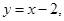 由
由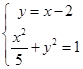 得:
得: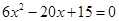 ,设
,设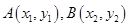 ,所以
,所以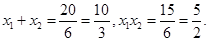 所以
所以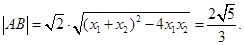
点评:直线与椭圆相交时求弦长往往离不开弦长公式,也离不开直线方程与椭圆方程联立方程组,一般运算量都比较大,要勤加练习,仔细运算.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
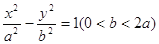 的左焦点
的左焦点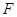 引圆
引圆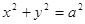 的切线,切点为T, 延长FT交双曲线右支于点P, O为坐标原点,M为PF 的中点,则
的切线,切点为T, 延长FT交双曲线右支于点P, O为坐标原点,M为PF 的中点,则 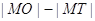 与
与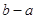 的大小关系为
的大小关系为 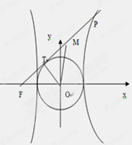
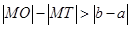
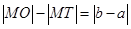
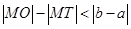
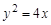 ,点P在此抛物线上,则P到直线
,点P在此抛物线上,则P到直线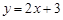 和
和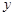 轴的距离之和的最小值
轴的距离之和的最小值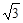
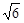
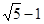
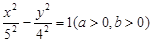 上一点,若
上一点,若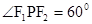 ,则三角形
,则三角形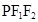 的面积为( )
的面积为( )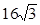
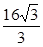
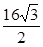
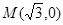 ,椭圆
,椭圆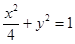 与直线
与直线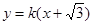 交于点
交于点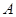 、
、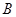 ,则
,则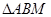 的周长为 .
的周长为 .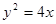 上有点
上有点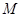 ,它到直线
,它到直线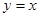 的距离为4
的距离为4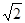 ,如果点
,如果点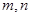 ),且
),且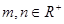 ,则
,则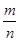 的值为( )
的值为( )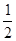
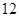 ,离心率为
,离心率为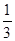 ,则椭圆的方程是( )
,则椭圆的方程是( )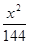 +
+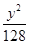 =1
=1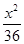 +
+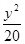 =1
=1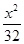 +
+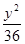 =1
=1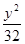 =1
=1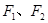 分别是双曲线
分别是双曲线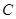 :
: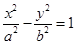 (
(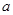 >0,
>0,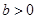 )的左、右焦点,
)的左、右焦点,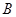 是虚轴的端点,直线
是虚轴的端点,直线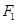
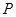 、
、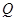 两点,线段
两点,线段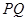 的垂直平分线与
的垂直平分线与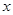 轴交于点
轴交于点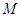 ,若
,若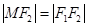 ,则
,则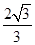
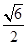
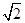
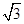
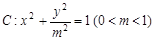 的左、右焦点分别为
的左、右焦点分别为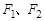 。过
。过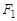 的直线
的直线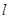 交
交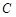 于
于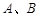 两点,且
两点,且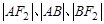 成等差数列.
成等差数列.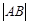 ; (2)若直线
; (2)若直线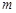 .
.