题目内容
17.若集合A={2,0},B={1,5},则A∩B=( )| A. | ∅ | B. | {0} | C. | {0,1} | D. | {2,0,1,5} |
分析 直接利用交集的运算法则求解即可.
解答 解:集合A={2,0},B={1,5},则A∩B=∅.
故选:A.
点评 本题考查集合的基本运算,考查计算能力.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
7.定义:$\frac{n}{{p}_{1}+{p}_{1}+…+{p}_{n}}$为n个p1,p2,…pn的“均倒数”,若已知正数数列{an}的前n项的”均倒数“为$\frac{1}{2n+1}$,又bn=$\frac{{a}_{n}-1}{2}$.,$\frac{1}{{b}_{1}{b}_{2}}$+$\frac{1}{{b}_{2}{b}_{3}}$+…+$\frac{1}{{b}_{2014}{b}_{2015}}$=( )
| A. | $\frac{2013}{4027}$ | B. | $\frac{4026}{4027}$ | C. | $\frac{2014}{4029}$ | D. | $\frac{4028}{4029}$ |
8.设集合A={x|x2-6x+8<0},B={x|2<2x<8},则A∩B=( )
| A. | {x|1<x<4} | B. | {x|1<x<3} | C. | {x|2<x<3} | D. | {x|3<x<4} |
2.某几何体的三视图如图所示,它的表面积为( )
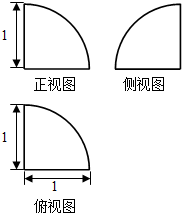

| A. | $\frac{π}{4}$ | B. | $\frac{5π}{4}$ | C. | $\frac{7π}{8}$ | D. | π |
9.甲、乙两人在2015年1月至5月的纯收入(单位:千元)的数据如下表:
(1)由表中数据直观分析,甲、乙两人中谁的纯收入较稳定?
(2)求y关于x的线性回归方程,并预测甲在6月份的纯收入;
(3)现从乙这5个月的纯收入中,随机抽取两个月,求恰有1个月的纯收入在区间(3,3.5)中的概率.
| 月份x | 1 | 2 | 3 | 4 | 5 |
| 甲的纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 |
| 乙的纯收入z | 2.8 | 3.4 | 3.8 | 4.5 | 5.5 |
(2)求y关于x的线性回归方程,并预测甲在6月份的纯收入;
(3)现从乙这5个月的纯收入中,随机抽取两个月,求恰有1个月的纯收入在区间(3,3.5)中的概率.
17.以平面直角坐标系的原点为极点,x轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位.已知直线l的参数方程为$\left\{\begin{array}{l}x=3-t\\ y=t-5\end{array}\right.$(t为参数),圆C的极坐标方程为ρ=4(cosθ+sinθ),则圆C上的点到直线l的距离的最大值为( )
| A. | 2$\sqrt{2}$ | B. | 3$\sqrt{2}$ | C. | 4$\sqrt{2}$ | D. | 5$\sqrt{2}$ |
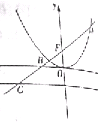 如图,过抛物线x2=2py(p>0)的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=$\sqrt{2}$|BF|,且|AF|=4+2$\sqrt{2}$,则p=2.
如图,过抛物线x2=2py(p>0)的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=$\sqrt{2}$|BF|,且|AF|=4+2$\sqrt{2}$,则p=2.