题目内容
18.求证:$\frac{1-2sinαcosα}{{{{cos}^2}α-{{sin}^2}α}}=tan(\frac{π}{4}-α)$.分析 利用同角三角函数的关系,结合差角的正切公式,即可证明结论.
解答 证明:左边=$\frac{(cosα-sinα)^{2}}{(cosα+sinα)(cosα-sinα)}$=$\frac{cosα-sinα}{cosα+sinα}$=$\frac{tan\frac{π}{4}-tanα}{1+tan\frac{π}{4}tanα}$=tan($\frac{π}{4}$-α)=右边,
所以$\frac{1-2sinαcosα}{{{{cos}^2}α-{{sin}^2}α}}=tan(\frac{π}{4}-α)$.
点评 本题考查同角三角函数的关系,差角的正切公式,考查学生分析解决问题的能力,比较基础.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
8.若sin($\frac{π}{5}$+θ)=$\frac{4}{5}$,则cos($\frac{2π}{5}$+2θ)=( )
| A. | $\frac{7}{25}$ | B. | $-\frac{7}{25}$ | C. | $\frac{24}{25}$ | D. | $-\frac{24}{25}$ |
9.设函数f(x)=$\left\{{\begin{array}{l}{{x^3}(0≤x<5)}\\{f(x-5)(x≥5)}\end{array}}$,那么f(2015)=( )
| A. | 27 | B. | 9 | C. | 0 | D. | 1 |
13.在△ABC中,角A,B,C成单调递增的等差数列,a,b,c是的△ABC三边,$b=\frac{{\sqrt{3}}}{2}$,则c-a的取值范围是( )
| A. | $(0,\frac{1}{4})$ | B. | $(0,\frac{{\sqrt{3}}}{2})$ | C. | $(0,\frac{1}{2})$ | D. | ($\frac{1}{4}$,$\frac{\sqrt{3}}{2}$) |
10.以下各式中错误的是( )
| A. | arcsin1=$\frac{π}{2}$ | B. | arccos(-1)=π | C. | arctan0=0 | D. | arccos1=2π |
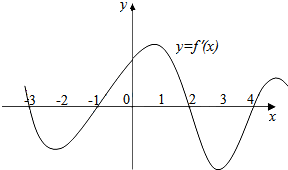 如图是y=f(x)的导函数的图象,现有四种说法:
如图是y=f(x)的导函数的图象,现有四种说法: