题目内容
15.甲、乙两同学的6次考试成绩分别为:| 甲 | 99 | 89 | 97 | 85 | 95 | 99 |
| 乙 | 89 | 93 | 90 | 89 | 92 | 90 |
(Ⅱ)计算甲、乙两同学考试成绩的方差,并对甲、乙两同学的考试成绩做出合理评价.
分析 (I)把两组数据的十位做茎,个位做叶,得到作出茎叶图.
(II)根据所给的数据先求出甲和乙的平均数,再求出两个人的方差,得到甲的方差比乙的方差要大,得到乙的成绩比较稳定.
解答 解:(Ⅰ)甲、乙两位同学六次考试成绩的茎叶图: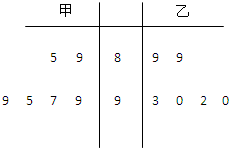
(Ⅱ)$\overline{x_甲}=\frac{99+89+97+85+95+99}{6}=94$,
$\overline{x_乙}=\frac{89+93+90+89+92+90}{6}=90.5$,
${s_甲}^2=\frac{1}{6}[(99-94{)^2}+(89-94{)^2}+(97-94{)^2}+(85-94{)^2}+(95-94{)^2}+(99-94{)^2}]=\frac{83}{3}=27\frac{2}{3}$,${s_乙}^2=\frac{1}{6}[(89-90.5{)^2}+(93-90.5{)^2}+(90-90.5{)^2}+(89-90.5{)^2}+(92-90.5{)^2}+(90-90.5{)^2}]=\frac{27}{2}=13\frac{1}{2}$,
评价:甲同学的平均水平要高于乙同学,但是甲同学的方差值较大,说明甲同学的发挥没有乙同学稳定.
点评 本题考查了茎叶图的知识以及平均数和方差的计算,属于基础题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
5.设$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$是单位向量,若$\overrightarrow{a}$=3$\overrightarrow{{e}_{1}}$,$\overrightarrow{b}$=$\overrightarrow{{e}_{1}}-\overrightarrow{{e}_{2}}$,$\overrightarrow{b}在\overrightarrow{a}$方向的投影为$\frac{1}{2}$,则$\overrightarrow{{e}_{1}}$与$\overrightarrow{{e}_{2}}$夹角为( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{5π}{6}$ |
6.已知点A(-1,1),B(-4,5),若$\overrightarrow{BC}=3\overrightarrow{BA}$,则点C的坐标为( )
| A. | (-10,13) | B. | (9,-12) | C. | (-5,7) | D. | (5,-7) |
3.i为虚数单位,则$|{\frac{1+i}{i}}|$等于( )
| A. | 1-i | B. | 1+i | C. | $\sqrt{2}$ | D. | 2 |
20.下列函数中,既是奇函数又在区间(0,+∞)上单调递增的函数是( )
| A. | y=x+x-1 | B. | y=x3+x | C. | y=2x+log2x | D. | $y={x^{\frac{1}{2}}}$ |
7.若数列{an},{bn}的通项公式分别是${a_n}={(-1)^{n+2014}}a$,${b_n}=2+\frac{{{{(-1)}^{n+2015}}}}{n}$,且an<bn对任意n∈N*恒成立,则实数a的取值范围是( )
| A. | [-1,$\frac{1}{2}$) | B. | [-2,$\frac{1}{2}$) | C. | [-2,$\frac{3}{2}$) | D. | [-1,$\frac{3}{2}$) |
20.已知数列{an},点{n,an}在函数$f(x)=sin(πx+\frac{π}{3})$的图象上,则a2015的值为( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |