题目内容
10.在△ABC中,AB边上的中线CO的长为4,若动点P满足$\overrightarrow{AP}={sin^2}θ•\overrightarrow{AO}+{cos^2}θ•\overrightarrow{AC}$(θ∈R),则$(\overrightarrow{PA}+\overrightarrow{PB})•\overrightarrow{PC}$的最小值是( )| A. | -9 | B. | -8 | C. | 4 | D. | 16 |
分析 如图所示,由动点P满足$\overrightarrow{AP}={sin^2}θ•\overrightarrow{AO}+{cos^2}θ•\overrightarrow{AC}$(θ∈R),利用向量共线定理可得:点P在线段CO上.利用基本不等式的性质可得:$(\overrightarrow{PA}+\overrightarrow{PB})•\overrightarrow{PC}$=2$\overrightarrow{PO}•\overrightarrow{PC}$≥-2$(\frac{|\overrightarrow{PC}|+|\overrightarrow{PO}|}{2})^{2}$.
解答 解:如图所示,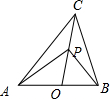
∵动点P满足$\overrightarrow{AP}={sin^2}θ•\overrightarrow{AO}+{cos^2}θ•\overrightarrow{AC}$(θ∈R),
sin2θ+cos2θ=1,sin2θ,cos2θ∈[0,1].
∴点P在线段CO上.
∴$(\overrightarrow{PA}+\overrightarrow{PB})•\overrightarrow{PC}$=2$\overrightarrow{PO}•\overrightarrow{PC}$≥-2$(\frac{|\overrightarrow{PC}|+|\overrightarrow{PO}|}{2})^{2}$=-2×22=-8,
当且仅当$\overrightarrow{PC}=-\overrightarrow{PO}$时取等号.
故选:B.
点评 本题考查了向量的平行四边形法则、向量共线定理、数量积运算性质、基本不等式的性质,考查了推理能力与计算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 15 | B. | 17 | C. | 19 | D. | 21 |
| 甲 | 99 | 89 | 97 | 85 | 95 | 99 |
| 乙 | 89 | 93 | 90 | 89 | 92 | 90 |
(Ⅱ)计算甲、乙两同学考试成绩的方差,并对甲、乙两同学的考试成绩做出合理评价.
| x | 0 | 1 | 2 | 3 |
| y=f(x) | 3 | 0 | 1 | 2 |
| x | 0 | 1 | 2 | 3 |
| y=g(x) | 1 | 0 | 3 | 2 |
| A. | a>b>c | B. | a>c>b | C. | b>c>a | D. | c>a>b |
 为了了解高一学生的体能情况,某校随机抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出了频率直方图如图所示,已知次数在[100,110)间的频数为7,次数在110以下(不含110)视为不达标,次数在[110,130)视为达标,次数在130以上视为有优秀.
为了了解高一学生的体能情况,某校随机抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出了频率直方图如图所示,已知次数在[100,110)间的频数为7,次数在110以下(不含110)视为不达标,次数在[110,130)视为达标,次数在130以上视为有优秀.