题目内容
在数列{an}中,a1=1,{an}的前n项和Sn满足2Sn=an+1.
(1)求数列{an}的通项公式;
(2)若存在n∈N*,使得λ≤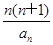 ,求实数λ的最大值.
,求实数λ的最大值.
(1)求数列{an}的通项公式;
(2)若存在n∈N*,使得λ≤
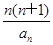 ,求实数λ的最大值.
,求实数λ的最大值.(1) an=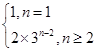 (2) 3
(2) 3
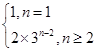 (2) 3
(2) 3(1)由题意,当n≥2时,2Sn-1=an,2Sn=an+1,
两式相减得2an=an+1-an,
即an+1=3an,又a2=2a1=2,
可见数列{an}从第二项起成公比为3的等比数列.
所以当n≥2时,an=a2·3n-2=2·3n-2,
故an=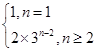
(2)令bn=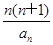 ,当n≥2时,bn=
,当n≥2时,bn=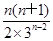
当n≥2时,bn+1-bn=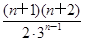 -
-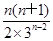 =
=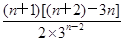 =
=
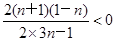 <0.
<0.
所以当n≥2时,bn+1<bn
所以,数列{bn}从第二项起的各项成单调递减数列
而b2=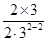 =3,b1=
=3,b1=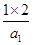 =2,
=2,
由题意,λ≤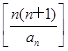 max=max{2,3}=3.
max=max{2,3}=3.
所求实数λ的最大值是3.
两式相减得2an=an+1-an,
即an+1=3an,又a2=2a1=2,
可见数列{an}从第二项起成公比为3的等比数列.
所以当n≥2时,an=a2·3n-2=2·3n-2,
故an=
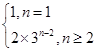
(2)令bn=
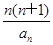 ,当n≥2时,bn=
,当n≥2时,bn=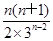
当n≥2时,bn+1-bn=
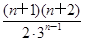 -
-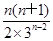 =
=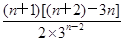 =
=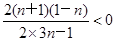 <0.
<0.所以当n≥2时,bn+1<bn
所以,数列{bn}从第二项起的各项成单调递减数列
而b2=
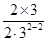 =3,b1=
=3,b1=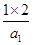 =2,
=2,由题意,λ≤
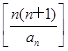 max=max{2,3}=3.
max=max{2,3}=3.所求实数λ的最大值是3.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
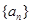 满足
满足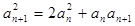 , 且
, 且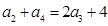 ,其中
,其中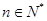 .
.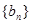 满足
满足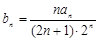 ,是否存在正整数
,是否存在正整数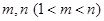 ,使得
,使得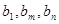 成等比数列?若存在,求出所有的
成等比数列?若存在,求出所有的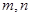 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。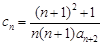 ,记数列
,记数列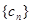 的前
的前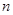 项和为
项和为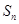 ,其中
,其中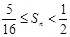 。
。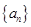 的前n项和记为
的前n项和记为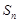 ,
,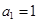 ,点
,点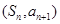 在直线
在直线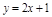 上,n∈N*.
上,n∈N*.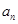 ;
;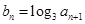 ,
,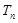 是数列
是数列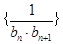 的前n项和,求
的前n项和,求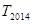 的值.
的值.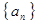 ,
,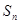 是其前
是其前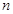 项的和,且满足
项的和,且满足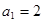 ,对一切
,对一切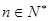 都有
都有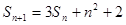 成立,设
成立,设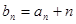 .
.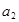 ;
;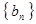 是等比数列;
是等比数列;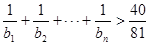 成立的最小正整数
成立的最小正整数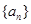 中,
中,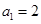 ,点
,点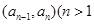 且
且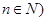 满足
满足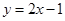 ,则
,则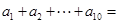 .
.