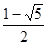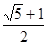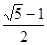题目内容
数列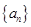 的前n项和记为
的前n项和记为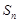 ,
,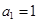 ,点
,点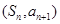 在直线
在直线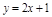 上,n∈N*.
上,n∈N*.
(1)求证:数列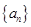 是等比数列,并求数列
是等比数列,并求数列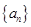 的通项公式
的通项公式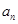 ;
;
(2)设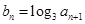 ,
,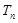 是数列
是数列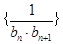 的前n项和,求
的前n项和,求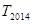 的值.
的值.
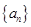 的前n项和记为
的前n项和记为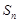 ,
,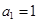 ,点
,点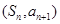 在直线
在直线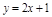 上,n∈N*.
上,n∈N*.(1)求证:数列
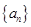 是等比数列,并求数列
是等比数列,并求数列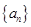 的通项公式
的通项公式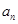 ;
;(2)设
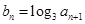 ,
,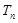 是数列
是数列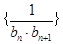 的前n项和,求
的前n项和,求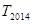 的值.
的值.(1)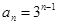 ;(2)
;(2)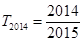 .
.
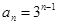 ;(2)
;(2)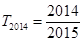 .
.试题分析:(1)求证:数列
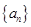 是等比数列,并求数列
是等比数列,并求数列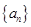 的通项公式
的通项公式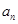 ,只需证明
,只需证明 等于一个与
等于一个与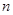 无关的常数,由已知点
无关的常数,由已知点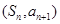 在直线
在直线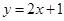 上,可得
上,可得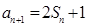 ,可利用
,可利用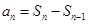 进行转化,即
进行转化,即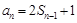
 ,由此可得
,由此可得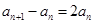 ,即
,即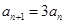
 ,可证得数列
,可证得数列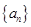 是等比数列,从而可求出数列
是等比数列,从而可求出数列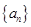 的通项公式
的通项公式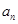 ;(2)设
;(2)设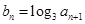 ,
,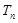 是数列
是数列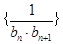 的前n项和,求
的前n项和,求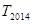 的值,首先求出数列
的值,首先求出数列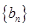 的通项公式
的通项公式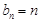 ,故数列
,故数列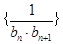 的通项公式为
的通项公式为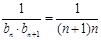 ,可用拆项相消法求和,即
,可用拆项相消法求和,即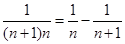 ,从而得
,从而得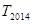 的值.
的值.试题解析:(1)由题意得
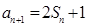 ,
,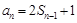
 ,(1分)两式相减,得
,(1分)两式相减,得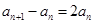 即
即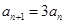
 ,(3分)
,(3分)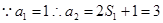 ,则
,则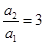 ,当
,当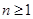 时
时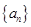 是首项为1,公比为3的等比数列.(5分)
是首项为1,公比为3的等比数列.(5分)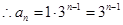 (6分)
(6分)(2)由(1)得知
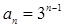 ,
,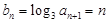 ,(8分)
,(8分) ,(10分)
,(10分)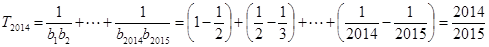 .(12分)
.(12分)
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
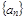 中,
中,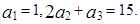
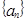 通项公式;
通项公式;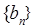 满足
满足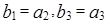 ,求数列
,求数列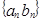 的前
的前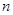 项和
项和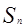 。
。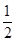 ,a4=-4,则|a1|+|a2|+…+|a6|=________.
,a4=-4,则|a1|+|a2|+…+|a6|=________.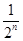 ,n∈N*,则:
,n∈N*,则: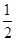
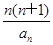 ,求实数λ的最大值.
,求实数λ的最大值.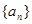 的公比
的公比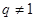 ,且
,且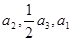 成等差数列,则
成等差数列,则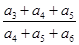 的值为( )
的值为( )