题目内容

10．观察正切函数的图象，满足|tanx|≤1的x的取值范围是 （　　）
A．[2kπ-$\frac{π}{4}$，2kπ+$\frac{π}{4}$]（k∈Z）B．[kπ，kπ+$\frac{π}{4}$]（k∈Z）
C．[kπ-$\frac{π}{4}$，kπ+$\frac{π}{4}$]（k∈Z）D．[kπ+$\frac{π}{4}$，kπ+$\frac{3π}{4}$]（k∈Z）

分析 把不等式化为-1≤tanx≤1，由正切函数的图象和性质解得即可．

解答 解：由|tanx|≤1得-1≤tanx≤1，
∴由正切函数y=tanx的性质得
kπ-$\frac{π}{4}$≤x＜kπ+$\frac{π}{4}$，
∴使不等式|tanx|≤1的x的取值范围是
[kπ-$\frac{π}{4}$，kπ+$\frac{π}{4}$]，k∈Z．
故选：C．

点评 本题考查了正切函数的图象与性质的应用问题，是基础题目．

练习册系列答案
相关题目
20．点M（2，1）关于直线x+y+1=0的对称点的坐标是（-2，-3）．
1．已知A，B分别为椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右顶点，点P为椭圆C上异于A，B的点，且直线PA，PB的斜率之积为-$\frac{5}{9}$，则椭圆C的离心率为$\frac{2}{3}$．
18．f（x）=ax2+bx+c满足f（0）=3，对称轴是直线x=-1，最小值为2，则该函数的表达式为（　　）
A．f（x）=x2-2x-3B．f（x）=x2+2x-3C．f（x）=x2-2x+3D．f（x）=x2+2x+3
5．设函数f（x）=ax2+bx+c（a≠0），对任意实数t都有f（2+t）=f（2-t）成立，给出以下说法：
（1）b=-4a；
（2）当a＞0且$\frac{m+n}{2}$＞2时，f（x）在区间[n，m]上的最大值为f（m）；
（3）无论a如何取值，函数值f（1），f（-1），f（$\frac{5}{2}$）中，最小的一个不可能是f（1）．
其中正确的个数为（　　）
A．0B．1C．2D．3
15．对于给定的函数f（x）=ax-a-x（x∈R，a＞0，且a≠1），下面给出五个命题，其中真命题是①③④（只需写出所有真命题的编号）
①函数f（x）的图象关于原点对称；
②函数f（x）在R上不具有单调性；
③函数f（|x|）的图象关于y轴对称；
④当0＜a＜1时，函数f（|x|）的最大值是0；
⑤当a＞1时，函数f（|x|）的最大值是0．
2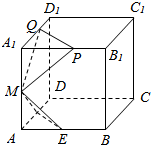．如图：已知棱长为l的正方体ABCD-A1B1C1D1中，E，F，M分别是AB、AD、AA1的中点，又P、Q分别在线段A1B1、A1D1上，且A1P=A1Q=x，0＜x＜1，设平面MEF∩平面MPQ=l，则下列结论中不成立的是（　　）
A．l∥平面ABCDB．平面MEF与平面MPQ不垂直
C．l⊥BC1D．当x变化时，l是定直线
19．已知集合U=R，A={x|3≤x＜7}，B={x|2＜x＜10}，C={x|x＞a}，
（1）求A∪B，（CUA）∩B；
（2）若A∩C=∅，求实数a的取值范围．
20．已知中心在坐标原点的椭圆和双曲线的焦点相同，左、右焦点分别为F1，F2，这两条曲线在第一象限的交点为P，且△PF1F2是以PF1为斜边的等腰直角三角形，则椭圆和双曲线的离心率之积为（　　）
A．1B．2$\sqrt{2}$+3C．2$\sqrt{2}$D．3一2$\sqrt{2}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网