题目内容
18．f（x）=ax2+bx+c满足f（0）=3，对称轴是直线x=-1，最小值为2，则该函数的表达式为（ ）| A． | f（x）=x2-2x-3 | B． | f（x）=x2+2x-3 | C． | f（x）=x2-2x+3 | D． | f（x）=x2+2x+3 |
分析 由二次函数f（x）=ax2+bx+c的对称轴直线x=-1，最小值为2，可得此二次函数的顶点坐标，然后利用顶点式求解即可．
解答 解：∵二次函数f（x）=ax2+bx+c的对称轴为x=-1，最小值为2，
∴此二次函数的顶点坐标为：（-1，2），
∴此二次函数为：f（x）=a（x+1）2+2，
∵f（0）=3，∴a+2=3，
解得：a=1，
∴此二次函数的解析式为：f（x）=（x+1）2+2=x2+2x+3．
故选：D．
点评 此题考查了待定系数法求函数的解析式．此题难度不大，注意掌握方程思想的应用．
练习册系列答案
每课必练系列答案
相关题目
10．观察正切函数的图象，满足|tanx|≤1的x的取值范围是 （ ）
| A． | [2kπ-$\frac{π}{4}$，2kπ+$\frac{π}{4}$]（k∈Z） | B． | [kπ，kπ+$\frac{π}{4}$]（k∈Z） | ||
| C． | [kπ-$\frac{π}{4}$，kπ+$\frac{π}{4}$]（k∈Z） | D． | [kπ+$\frac{π}{4}$，kπ+$\frac{3π}{4}$]（k∈Z） |
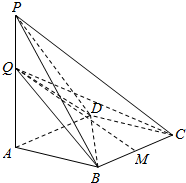已知四棱锥P-ABCD中，底面ABCD为∠ABC=$\frac{2}{3}$π的菱形，PA⊥平面ABCD，点Q在直线PA上．
8．若x＞1，则函数y=$\frac{{{x^2}+x+2}}{x-1}$的最小值为（ ）
| A． | 4 | B． | 5 | C． | 6 | D． | 7 |