题目内容
【题目】已知圆M：
，直线l：
，A为直线l上一点．
若
，过A作圆M的两条切线，切点分别为P，Q，求
的大小；
若圆M上存在两点B，C，使得
，求点A横坐标的取值范围．
【答案】（1）
（2）
【解析】
确定
是等腰直角三角形，可得
，同理得
，即可求
的大小；
从直线上的点向圆上的点连线成角，当且仅当两条线均为切线时才是最大的角，不妨设切线为AP，AQ，则为
时，
为
，所以MA的长度为4，故可确定点A的横坐标
的取值范围．
由题知
，即AM为M点到直线l的距离，
，
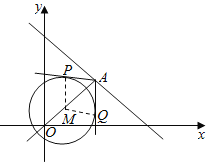
在直角三角形APM中，
，
，
是等腰直角三角形，
，
同理得
由题意，从直线上的点向圆上的点连线成角，
当且仅当两条线均为切线时才是最大的角，
不妨设切线为AP，AQ，则为时，为，所以MA的长度为4，
故问题转化为在直线上找到一点，使它到点M的距离为4．
设
，则
，
或5
点A的横坐标的取值范围是
练习册系列答案
相关题目
