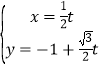[题目]在平面直角坐标系中.以原点为极点.x轴为极轴建立极坐标系.曲线C1的方程为 .曲线C2的极坐标方程为C2:ρcosθ+ρsinθ=1.若曲线C1与C2相交于A.B两点．(1)求|AB|的值,到A.B两点的距离之积．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】在平面直角坐标系中，以原点为极点，x轴为极轴建立极坐标系，曲线C1的方程为（θ为参数），曲线C2的极坐标方程为C2：ρcosθ+ρsinθ=1，若曲线C1与C2相交于A、B两点．
（1）求|AB|的值；
（2）求点M（﹣1，2）到A、B两点的距离之积．

【答案】
（1）解：曲线C1的方程为 =1，C2：ρcosθ+ρsinθ=1，

则C2的普通方程为x+y﹣1=0，

则C2的参数方程为，

代入C1得2t2+7 t+10=0，

∴|AB|=|t1﹣t2|= =

（2）解：|MA||MB|=|t1t2|=5
【解析】（1）先求出C1的普通方程和C2的参数方程，再根据韦达定理和弦长公式即可求出，（2）直接由（1）即可求出答案．

练习册系列答案

名校课堂系列答案

十二进制	0	1	2	3	4	5	6	7	8	9	M	N
十进制	0	1	2	3	4	5	6	7	8	9	10	11

例如，因为563＝3×122＋10×12＋11，所以十进制中的563在十二进制中被表示为3MN(12)．那么十进制中的2008在十二进制中被表示为(　　)

A. 11N4(12) B. 1N25(12) C. 12N4(12) D. 1N24(12)

【题目】已知圆M：，直线l：，A为直线l上一点．

若，过A作圆M的两条切线，切点分别为P，Q，求的大小；

若圆M上存在两点B，C，使得，求点A横坐标的取值范围．

【题目】已知cos（α﹣β）=﹣ ，cos（α+β）= ，且（α﹣β）∈（，π），（α+β）∈（，2π），则cos2α=（）
A.﹣1
B.﹣
C.
D.﹣

【题目】已知函数f（x）= sin2x+ sin2x．
（1）求函数f（x）的单调递减区间；
（2）在△ABC中，角A，B，C的对边分别为a，b，c，若f（）= ，△ABC的面积为3 ，求a的最小值．

（Ⅰ）从这5天中任选2天，记发芽的种子数分别为m，n，求事件“m，n均不小于25”的概率．
（Ⅱ）从这5天中任选2天，若选取的是4月1日与4月30日的两组数据，请根据这5天中的另3天的数据，求出y关于x的线性回归方程 = x+ ．
（参考公式： = ， = ﹣ ）

【题目】已知函f（x）=ax2﹣ex（a∈R）．（Ⅰ）a=1时，试判断f（x）的单调性并给予证明；
（Ⅱ）若f（x）有两个极值点x1 ， x2（x1＜x2）．
（i）求实数a的取值范围；
（ii）证明：﹣ ．（注：e是自然对数的底数）

【题目】在平面直角坐标系中，曲线过点，其参数方程为（为参数，），以为极点，轴非负半轴为极轴，建立极坐标系，曲线的极坐标方程为.

（1）求曲线的普通方程和曲线的直角坐标方程；

（2）求已知曲线和曲线交于两点，且，求实数的值.

【题目】在直角坐标系中，曲线的参数方程为（为参数），直线的参数方程为（为参数），且直线与曲线交于两点，以直角坐标系的原点为极点，以轴的正半轴为极轴建立极坐标系.

（1）求曲线的极坐标方程；

（2）已知点的极坐标为，求的值

试题分类