题目内容
【题目】如图,在四面体
中, 
在平面
的射影
为棱
的中点, 
为棱
的中点,过直线
作一个平面与平面
平行,且与
交于点
,已知
, 
.
(1)证明: 为线段的中点
(2)求平面与平面
所成锐二面角的余弦值.
【答案】（1）见解析（2）
【解析】分析：(1)根据题中两面平行的条件，结合面面平行的性质，得到线线平行，其中一个点是中点，那就是三角形的中位线，从而得到一定为中点；
(2)利用题中所给的相关的垂直的条件，建立相应的坐标系，求得面的法向量，利用法向量所成角的余弦值得到对应二面角的余弦值.
详解：(1)证明: 
平面
平面
，
平面
平面
，
平面
平面
，
，
为
的中点, 
为
的中点.
(2)解: 
为的中点, 
，
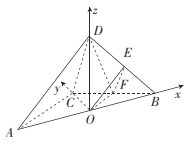
以
为坐标原点,建立空间直角坐标系
，如图所示,则
，
，
，
易求得
，
，
设平面
的法向量为
，则
，
即
，
令
，得
.
设平面
的法向量为
，则
，即
，
令
，得
，
又平面平面，
平面与平面所成锐二面角的余弦值为.
练习册系列答案
相关题目
【题目】类似于十进制中的逢10进1，十二进制的进位原则是逢12进1，采用数字0，1，2，…，9和字母M，N作为计数符号，这些符号与十进制的数字对应关系如下表：
十二进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | M | N |
十进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
例如，因为563＝3×122＋10×12＋11，所以十进制中的563在十二进制中被表示为3MN(12)．那么十进制中的2008在十二进制中被表示为( )
A. 11N4(12) B. 1N25(12) C. 12N4(12) D. 1N24(12)
