题目内容
【题目】某工厂2016年计划生产A、B两种不同产品,产品总数不超过300件,生产产品的总费用不超过9万元.A、B两个产品的生产成本分别为每件500元和每件200元,假定该工厂生产的A、B两种产品都能销售出去,A、B两种产品每件能给公司带来的收益分别为0.3万元和0.2万元.问该工厂如何分配A、B两种产品的生产数量,才能使工厂的收益最大?最大收益是多少万元?
【答案】解:设工厂生产A、B两种产品分别为x件和y件,总收益为z元, 由题意得 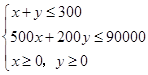 ,
,
目标函数z=3000x+2000x.
二元一次不等式组等价于 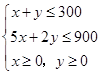 .
.
作出二元一次不等式组所表示的平面区域,即可行域,如图阴影部分.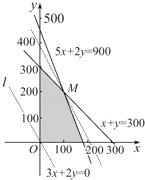
作直线l:3000x+2000y=0,即3x+2y=0,
平移直线l,从图中可知,当直线过M点时,目标函数取得最大值.
联立 ![]() ,解得
,解得 ![]() .
.
∴点的坐标为(100,200),此时zmax=3000×100+2000×200=700000.
∴该工厂生产A产品100件,生产B产品200件时收益最大,最大收益是70万元.
【解析】设工厂生产A、B两种产品分别为x件和y件,总收益为z元,由题意作出约束条件并化简,得到目标函数z=3000x+2000x.作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,把最优解的坐标代入目标函数得答案.

【题目】类似于十进制中的逢10进1,十二进制的进位原则是逢12进1,采用数字0,1,2,…,9和字母M,N作为计数符号,这些符号与十进制的数字对应关系如下表:
十二进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | M | N |
十进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
例如,因为563=3×122+10×12+11,所以十进制中的563在十二进制中被表示为3MN(12).那么十进制中的2008在十二进制中被表示为( )
A. 11N4(12) B. 1N25(12) C. 12N4(12) D. 1N24(12)



