题目内容
13.已知正四棱柱底面边长为1高为2,俯视图是一个面积为1的正方形,则该正四棱锥的正视图的面积不可能等于( )| A. | 2 | B. | 2.5 | C. | 2$\sqrt{3}$-1 | D. | 2$\sqrt{2}$+1 |
分析 根据正四棱柱的正视图的边长变化,求出正视图的面积的取值范围即可判断.
解答 解:∵正四棱柱的俯视图是一个面积为1的正方形,
∴正方形的边长为1,正方形的对角线长为$\sqrt{2}$,
∵棱柱的高为2,
∴当正方形的边长作为正视图的底面边长时,此时面积的最小值为S=2×1=2,
当正方形的对角线作为正视图的底面边长时,此时面积的最大值为S=2×$\sqrt{2}$=2$\sqrt{2}$,
∴正四棱的正视图的面积S的取值范围是[2,2$\sqrt{2}$].
∵2$\sqrt{2}$+1∉[2,2$\sqrt{2}$],
∴D不成立,
故选:D.
点评 本题主要考查正四棱柱正视图的取值范围,根据不同的视角,得到正视图对应矩形的面积的最大值和最小值是解决本题的关键,利用函数的角度研究面积的取值范围是解决本题的突破点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.某人捡到不规则形状的五面体石块,他在每个面上作了记号,投掷了100次,并且记录了每个面落在桌面上的次数(如表),如果再投掷一次,请估计石块的第4面落在桌面上的概率是多少?
| 石块的面 | 1 | 2 | 3 | 4 | 5 |
| 频数 | 32 | 18 | 15 | 13 | 22 |
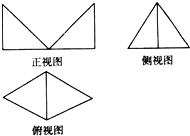 某几何体的三视图如图,其侧视图是一个边长为1的等边三角形,俯视图是由两个等边三角形拼成,则该几何体的体积为$\frac{1}{4}$.
某几何体的三视图如图,其侧视图是一个边长为1的等边三角形,俯视图是由两个等边三角形拼成,则该几何体的体积为$\frac{1}{4}$.