题目内容
【题目】已知定义域为![]() 的函数
的函数![]() 是奇函数.
是奇函数.
(1) 求实数![]() 的值;
的值;
(2) 判断并用定义证明该函数在定义域![]() 上的单调性;
上的单调性;
(3) 若方程![]() 在
在![]() 内有解,求实数
内有解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)1;(2)见解析;(3)[-1,3).
【解析】
(1)根据![]() 解得
解得![]() ,再利用奇偶性的定义验证,即可求得实数
,再利用奇偶性的定义验证,即可求得实数![]() 的值;(2)先对
的值;(2)先对![]() 分离常数
分离常数![]() 后,判断出
后,判断出![]() 为递减函数,再利用单调性的定义作差证明即可;(3)先用函数的奇函数性质,再用减函数性质变形,然后分离参数
为递减函数,再利用单调性的定义作差证明即可;(3)先用函数的奇函数性质,再用减函数性质变形,然后分离参数![]() 可得,
可得,![]() 在
在![]() 内有解,令
内有解,令![]() ,只要
,只要![]() .
.
(1)依题意得,![]() ,故
,故![]() ,此时
,此时![]() ,
,
对任意![]() 均有
均有![]() ,
,
所以![]() 是奇函数,所以
是奇函数,所以![]() .
.
(2)![]() 在
在![]() 上是减函数,证明如下:任取
上是减函数,证明如下:任取![]() ,则
,则
![]()
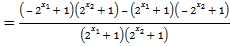
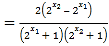
![]()
所以该函数在定义域![]() 上是减函数.
上是减函数.
(3)由函数![]() 为奇函数知,
为奇函数知,
![]() ,
,
又函数![]() 是单调递减函数,从而
是单调递减函数,从而![]() ,
,
即方程![]() 在
在![]() 内有解,
内有解,
令![]() ,只要
,只要![]() ,
,
![]() , 且
, 且![]() ,∴
,∴![]()
∴当![]() 时,原方程在
时,原方程在![]() 内有解.
内有解.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
【题目】已知某海滨浴场海浪的高度y(米)是时间t(0≤t≤24,单位:时)的函数,记作:![]() .下表是某日各时的浪高数据.
.下表是某日各时的浪高数据.
t(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
y(米) | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1.0 | 0.5 | 0.99 | 1.5 |
(1)根据以上数据,求函数y=f(t)的函数表达式;
(2)依据规定,当海浪高度高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的上午8:00时至晚上20:00时之间,有多少时间可供冲浪者进行运动?