题目内容
【题目】已知![]() 是定义域为
是定义域为![]() 的奇函数,且
的奇函数,且![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)证明![]() 在区间
在区间![]() 上是增函数;
上是增函数;
(3)求不等式![]() 的解集.
的解集.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() .
.
【解析】试题分析:(1)由![]() 是定义域为
是定义域为![]() 的奇函数可得
的奇函数可得![]() ,再由
,再由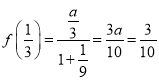 ,解得
,解得![]() ,可求函数
,可求函数![]() 的解析式;(2)任取
的解析式;(2)任取![]() ,将
,将![]() 分解因式,可证明
分解因式,可证明![]() ,从而可得结论;(3)根据
,从而可得结论;(3)根据![]() 在区间
在区间![]() 上是增函数,结合函数的定义域列不等式组求解即可.
上是增函数,结合函数的定义域列不等式组求解即可.
试题解析:(1)由题意可得![]() ,∴
,∴![]() ,
,
∴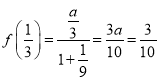 ,解得
,解得![]() ,∴
,∴![]() .
.
(2)设![]() ,则
,则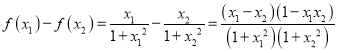 ,
,
∵![]() ,∴
,∴![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,即
,即![]() ,∴
,∴![]() 在
在![]() 上是增函数.
上是增函数.
(3)由![]() 得
得![]() ,即
,即![]() ,
,
由已知及(2)可得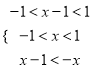 ,解得
,解得![]() ,
,
∴原不等式的解集为![]() .
.
【方法点晴】本题主要考查抽象函数的定义域、函数的单调性及利用单调性函数解不等式,属于难题. 利用单调性函数解不等式应注意以下三点:(1)一定注意函数的定义域(这一点是同学们容易疏忽的地方,不能掉以轻心);(2)注意应用函数的奇偶性(往往需要先证明是奇函数还是偶函数);(3)化成![]() 后再利用单调性和定义域列不等式组..
后再利用单调性和定义域列不等式组..

练习册系列答案
相关题目
【题目】某市春节期间7家超市的广告费支出![]() (万元)和销售额
(万元)和销售额![]() (万元)数据如下:
(万元)数据如下:
超市 | A | B | C | D | E | F | G |
广告费支出 | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
销售额 | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
(1)若用线性回归模型拟合![]() 与
与![]() 的关系,求
的关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)用二次函数回归模型拟合![]() 与
与![]() 的关系,可得回归方程:
的关系,可得回归方程:![]() ,
,
经计算二次函数回归模型和线性回归模型的![]() 分别约为
分别约为![]() 和
和![]() ,请用
,请用![]() 说明选择哪个回归模型更合适,并用此模型预测
说明选择哪个回归模型更合适,并用此模型预测![]() 超市广告费支出为3万元时的销售额.
超市广告费支出为3万元时的销售额.
参数数据及公式:![]() ,
,![]() ,
,
 .
.
