题目内容
【题目】圆(x－3) 2＋(y＋4) 2＝1关于直线x＋y＝0对称的圆的方程是( )
A. (x＋3)2＋(y－4)2＝1
B. (x－4)2＋(y＋3)2＝1
C. (x＋4)2＋(y－3)2＝1
D. (x－3)2＋(y－4)2＝1
【答案】B
【解析】
圆（x﹣3）2+（y+4）2=1的圆心A（3，﹣4），半径r=1，设圆心A（3，﹣4），关于直线x+y=0对称的圆心B（a，b），则直线x+y=0是线段AB的垂直平分线，由此求出点B的坐标，从而能够求出圆（x﹣3）2+（y+4）2=1关于直线x+y=0对称的圆方程．
圆（x﹣3）2+（y+4）2=1的圆心A（3，﹣4），半径r=1，
设圆心A（3，﹣4），关于直线x+y=0对称的圆心B（a，b），
则直线x+y=0是线段AB的垂直平分线，
∴AB的直线方程为：y+4=x﹣3，即x﹣y﹣7=0，
解方程组
，得线段AB的中点坐标为（
），
∴
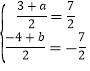，解得a=4，b=﹣3，
∴圆（x﹣3）2+（y+4）2=1关于直线x+y=0对称的圆方程是（x﹣4）2+（y+3）2=1．
故答案为：B
练习册系列答案
相关题目
