Question

【题目】已知函数．

（1）求f（x）的定义域和值域；

（2）判断f（x）的奇偶性与单调性；

（3）解关于x的不等式f（x2﹣2x+2）+f（﹣5）＜0．

Answer 1

【答案】（1）定义域R,值域为；（2）见解析；（3）

【解析】

（1）将函数看作方程，解得，再由2x＞0，解得y的范围，即为所求；（2）函数f（x）的定义域为R，由f（﹣x）＝﹣f（x），推出f（x）是奇函数；利用函数单调性的定义证明函数f（x）在（-∞，+∞）上单调递增；（3）利用f（x）为奇函数把不等式转化为f（x2﹣2x+2）＜f（5），再根据其单调性即可得到不等式的解集．

（1）f（x）的定义域是R，令y=，得2x=﹣．

∵2x＞0，∴﹣＞0，解得﹣1＜y＜1．

∴f（x）的值域为{y|﹣1＜y＜1}；

（2）∵f（﹣x）===﹣f（x），∴f（x）是奇函数．

∵f（x）==1﹣，在R上任取x1，x2，且x1＜x2，

f（x1）﹣f（x2）==，

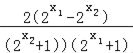∵x1＜x2，∴，（2x1+1）＞0，

即有f（x1）＜f（x2），则f（x）在R上是增函数．

（3）由（2）得f（x）是奇函数，且f（x）在R上是增函数．

则f（x2﹣2x+2）+f（﹣5）＜0即为f（x2﹣2x+2）＜﹣f（﹣5）=f（5），

得x2﹣2x+2＜5，即有x2﹣2x﹣3＜0，

解得﹣1＜x＜3，则不等式解集为（﹣1，3）．