题目内容
【题目】如图,F1、F2分别是双曲线 ![]() =1(a>0,b>0)的两个焦点,以坐标原点O为圆心,|OF1|为半径的圆与该双曲线左支交于A、B两点,若△F2AB是等边三角形,则双曲线的离心率为 ( )
=1(a>0,b>0)的两个焦点,以坐标原点O为圆心,|OF1|为半径的圆与该双曲线左支交于A、B两点,若△F2AB是等边三角形,则双曲线的离心率为 ( ) 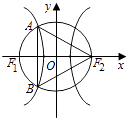
A.![]()
B.2
C.![]() ﹣1
﹣1
D.1+ ![]()
【答案】D
【解析】解:连结AF1 ,
∵F1F2是圆O的直径,
∴∠F1AF2=90°,即F1A⊥AF2 ,
又∵△F2AB是等边三角形,F1F2⊥AB,
∴∠AF2F1= ![]() ∠AF2B=30°,
∠AF2B=30°,
因此,Rt△F1AF2中,|F1F2|=2c,|F1A|= ![]() |F1F2|=c,
|F1F2|=c,
|F2A|= ![]() |F1F2|=
|F1F2|= ![]() c.
c.
根据双曲线的定义,得2a=|F2A|﹣|F1A|=( ![]() ﹣1)c,
﹣1)c,
解得c=( ![]() +1)a,
+1)a,
∴双曲线的离心率为e= ![]() =
= ![]() +1.
+1.
故选D.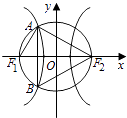

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
【题目】从某校随机抽取200名学生,获得了他们一周课外阅读时间(单位:h)的数据,整理得到数据的频数分布表和频率分布直方图(如图).
编 号 | 分 组 | 频 数 |
1 | [0,2) | 12 |
2 | [2,4) | 16 |
3 | [4,6) | 34 |
4 | [6,8) | 44 |
续 表
编 号 | 分 组 | 频 数 |
5 | [8,10) | 50 |
6 | [10,12) | 24 |
7 | [12,14) | 12 |
8 | [14,16) | 4 |
9 | [16,18] | 4 |
合计 | 200 |

(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12 h的概率;
(2)求频率分布直方图中的a,b的值;
(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的200名学生该周课外阅读时间的平均数在第几组.