题目内容
【题目】如图1,在直角梯形ABCD中,AD∥BC,∠BAD=![]() ,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点,将△ABE沿BE折起到△A1BE的位置,如图2.
,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点,将△ABE沿BE折起到△A1BE的位置,如图2.
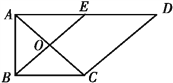
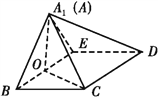
图1 图2
(1)证明:CD⊥平面A1OC;
(2)若平面A1BE⊥平面BCDE,求平面A1BC与平面A1CD夹角的余弦值.
【答案】(1) 见解析;(2) ![]()
【解析】试题分析:(1)折起后![]() , 根据线面垂直的判定定理可得
, 根据线面垂直的判定定理可得![]() 平面
平面![]() ,即可证明
,即可证明![]() 平面
平面![]() ;(2)若平面
;(2)若平面![]() 平面
平面![]() ,根据(1)可得
,根据(1)可得![]() 两两垂直,以
两两垂直,以 ![]() 建立空间坐标系,利用向量垂直数量积为零,分别求出平面
建立空间坐标系,利用向量垂直数量积为零,分别求出平面![]() 与平面
与平面![]() 的法向量,根据空间向量夹角余弦公式可得结果.
的法向量,根据空间向量夹角余弦公式可得结果.
试题解析:(1) 在题图1中,因为AB=BC=1,AD=2,E是AD的中点,∠BAD=![]() AD∥BC,
AD∥BC,
所以BE⊥AC,BE∥CD,
即在题图2中,BE⊥OA1,BE⊥OC,且OA1∩OC=O,
从而BE⊥平面A1OC,
又CD∥BE,
所以CD⊥平面A1OC.
(2)解:因为平面A1BE⊥平面BCDE,
又由(1)知BE⊥OA1,BE⊥OC,
所以∠A1OC为二面角A1BEC的平面角,
所以∠A1OC=![]() .
.
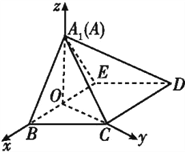
如图,以O为原点,建立空间直角坐标系,
因为A1B=A1E=BC=ED=1,
BC∥ED,
所以B
(![]() ,0,0),E(-
,0,0),E(- ![]() ,0,0),
,0,0),
A1(0,0, ![]() ),C(0,
),C(0, ![]() ,0),
,0),
得![]() =(-
=(-![]() ,
, ![]() ,0),
,0), ![]() =(0,
=(0, ![]() ,-
,-![]() ),
),
![]() =
=![]() (-
(-![]() ,0,0).
,0,0).
设平面A1BC的法向量n1=(x1,y1,z1),
平面A1CD的法向量n2=(x2,y2,z2),平面A1BC与平面A1CD夹角为θ,
则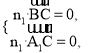
得![]()
取n1=(1,1,1); 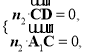
得![]()
取n2=(0,1,1),
从而cos θ=|cos<n1,n2>|=![]() =
=![]() ,
,
即平面A1BC与平面A1CD夹角的余弦值为![]() .
.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案【题目】从某校随机抽取200名学生,获得了他们一周课外阅读时间(单位:h)的数据,整理得到数据的频数分布表和频率分布直方图(如图).
编 号 | 分 组 | 频 数 |
1 | [0,2) | 12 |
2 | [2,4) | 16 |
3 | [4,6) | 34 |
4 | [6,8) | 44 |
续 表
编 号 | 分 组 | 频 数 |
5 | [8,10) | 50 |
6 | [10,12) | 24 |
7 | [12,14) | 12 |
8 | [14,16) | 4 |
9 | [16,18] | 4 |
合计 | 200 |

(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12 h的概率;
(2)求频率分布直方图中的a,b的值;
(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的200名学生该周课外阅读时间的平均数在第几组.
【题目】把单位正方体的六个面分别染上6种颜色,并画上个数不同的金鸡,各面的颜色与鸡的个数对应如表:
面上所染颜色 | 红 | 黄 | 蓝 | 青 | 紫 | 绿 |
该面上的金鸡个数 | 1 | 2 | 3 | 4 | 5 | 6 |
取同样的4个上述的单位正方体拼成一个如图所示的水平放置的长方体.则这个长方体的下底面总计画有______个金鸡


