题目内容
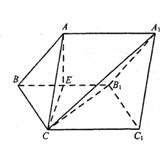
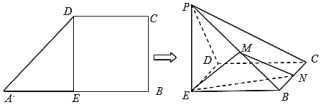
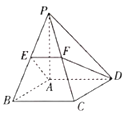
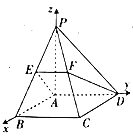
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,四边形
,四边形![]() 为正方形,点
为正方形,点![]() 为线段
为线段![]() 上的点,过
上的点,过![]() 三点的平面与
三点的平面与![]() 交于点
交于点![]() .将①
.将①![]() ,②
,②![]() ,③
,③![]() 中的两个补充到已知条件中,解答下列问题:
中的两个补充到已知条件中,解答下列问题:
(1)求平面![]() 将四棱锥分成两部分的体积比;
将四棱锥分成两部分的体积比;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
若补充②③根据已知可得![]() 平面
平面![]() ,从而有
,从而有![]() ,结合
,结合![]() ,可得
,可得
![]() 平面
平面![]() ,故有
,故有![]() ,而
,而![]() ,得到
,得到![]() ,②③成立与①②相同,
,②③成立与①②相同,
①③成立,可得![]() ,所以任意补充两个条件,结果都一样,以①②作为条件分析;
,所以任意补充两个条件,结果都一样,以①②作为条件分析;
(1)设![]() ,可得
,可得![]() ,进而求出梯形
,进而求出梯形![]() 的面积,可求出
的面积,可求出![]() ,即可求出结论;
,即可求出结论;
(2)![]() ,以
,以![]() 为坐标原点,建立空间坐标系,求出
为坐标原点,建立空间坐标系,求出![]() 坐标,由(1)得
坐标,由(1)得![]() 为平面
为平面![]() 的法向量,根据空间向量的线面角公式即可求解.
的法向量,根据空间向量的线面角公式即可求解.
第一种情况:若将①![]() ,②
,②![]() 作为已知条件,解答如下:
作为已知条件,解答如下:
(1)设平面![]() 为平面
为平面![]() .
.
∵![]() ,∴
,∴![]() 平面
平面![]() ,而平面
,而平面![]() 平面
平面![]() ,
,
∴![]() ,又
,又![]() 为
为![]() 中点.
中点.
设![]() ,则
,则![]() .
.
在三角形![]() 中,
中,![]() ,
,
由![]() 知
知![]() 平面
平面![]() ,
,
∴![]() ,
,
∴梯形![]() 的面积
的面积
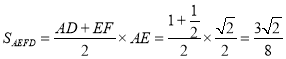 ,
,
![]() ,
,![]() ,
,
![]() 平面
平面![]() ,
,
![]() ,
,![]() ,
,
∴![]() ,
,
故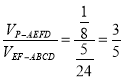 ,
,![]() .
.
(2)如图,分别以![]() 所在直线为
所在直线为![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
设![]() ,则
,则![]()
![]() ,
,
由(1)得![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
因为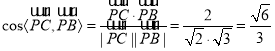 ,
,
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
第二种情况:若将①![]() ,③
,③![]() 作为已知条件,
作为已知条件,
则由![]() 知
知![]() 平面
平面![]() ,
,![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ,
,![]() ,
,
又![]() ,故
,故![]() 为
为![]() 中点,即
中点,即![]() ,解答如上不变.
,解答如上不变.
第三种情况:若将②![]() ,③
,③![]() 作为已知条件,
作为已知条件,
由![]() 及第二种情况知
及第二种情况知![]() ,又
,又![]() ,
,
易知![]() ,解答仍如上不变.
,解答仍如上不变.

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案【题目】某地区为了调查高粱的高度、粒的颜色与产量的关系,对700棵高粱进行抽样调查,得到高度频数分布表如下:
表1:红粒高粱频数分布表
农作物高度( |
|
|
|
|
|
|
频数 | 2 | 5 | 14 | 13 | 4 | 2 |
表2:白粒高粱频数分布表
农作物高度( |
|
|
|
|
|
|
频数 | 1 | 7 | 12 | 6 | 3 | 1 |
(1)估计这700棵高粱中红粒高粱的棵数;画出这700棵高粱中红粒高粱的频率分布直方图;
(2)①估计这700棵高粱中高粱高(cm)在![]() 的概率;②在红粒高粱中,从高度(单位:cm)在
的概率;②在红粒高粱中,从高度(单位:cm)在![]() 中任选3棵,设
中任选3棵,设![]() 表示所选3棵中高(单位:cm)在
表示所选3棵中高(单位:cm)在![]() 的棵数,求
的棵数,求![]() 的分布列和数学期望.
的分布列和数学期望.