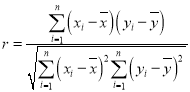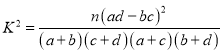题目内容
【题目】设函数![]() ,其中
,其中![]() 为正实数.
为正实数.
(1)若不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,证明
时,证明![]() .
.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)讨论研究函数![]() 的单调性,求出函数
的单调性,求出函数![]() 在
在![]() 上的最大值.要不等式
上的最大值.要不等式![]() 恒成立,只需最大值小于零,即可求出.
恒成立,只需最大值小于零,即可求出.
(2)将原不等式等价变形为![]() ,由(1)可知
,由(1)可知![]() ,试证
,试证![]() 在
在![]() 时恒成立,即可由不等式性质证出
时恒成立,即可由不等式性质证出![]() .
.
(1)由题意得![]()
设![]() ,则
,则![]() ,
,
①当![]() 时,即
时,即![]() 时,
时,![]() ,
,
所以函数![]() 在
在![]() 上单调递增,
上单调递增,![]() ,满足题意;
,满足题意;
②当![]() 时,即
时,即![]() 时,则
时,则![]() 的图象的对称轴
的图象的对称轴![]()
因为![]() ,
,
所以![]() 在
在![]() 上存在唯一实根,设为
上存在唯一实根,设为![]() ,则当
,则当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
此时![]() ,不合题意.
,不合题意.
综上可得,实数![]() 的取值范围是
的取值范围是![]() .
.
(2)![]() 等价于
等价于![]()
因为![]() ,所以
,所以![]() ,所以原不等式等价于
,所以原不等式等价于![]() ,
,
由(1)知当![]() 时,
时,![]() 在
在![]() 上恒成立,整理得
上恒成立,整理得![]()
令![]() ,则
,则 ,
,
所以函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
所以![]() ,即
,即![]() 在
在![]() 上恒成立.
上恒成立.
所以,当![]() 时,恒有
时,恒有![]() ,
,

练习册系列答案
相关题目
【题目】生男生女都一样,女儿也是传后人.由于某些地区仍然存在封建传统思想,头胎的男女情况可能会影响生二孩的意愿,现随机抽取某地200户家庭进行调查统计.这200户家庭中,头胎为女孩的频率为0.5,生二孩的频率为0.525,其中头胎生女孩且生二孩的家庭数为60.
(1)完成下列![]() 列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
生二孩 | 不生二孩 | 合计 | |
头胎为女孩 | 60 | ||
头胎为男孩 | |||
合计 | 200 |
(2)在抽取的200户家庭的样本中,按照分层抽样的方法在生二孩的家庭中抽取了7户,进一步了解情况,在抽取的7户中再随机抽取4户,求抽到的头胎是女孩的家庭户数![]() 的分布列及数学期望.
的分布列及数学期望.
附:
| 0.15 | 0.05 | 0.01 | 0.001 |
| 2.072 | 3.841 | 6.635 | 10.828 |
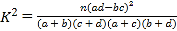 (其中
(其中![]() ).
).