题目内容
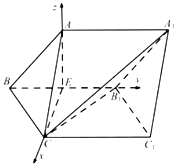
【题目】如图，三棱柱ABC-A1B1C1中，侧面BCC1B1是菱形，AC=BC=2，∠CBB1=
，点A在平面BCC1B1上的投影为棱BB1的中点E．
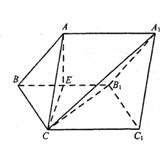
（1）求证：四边形ACC1A1为矩形；
（2）求二面角E-B1C-A1的平面角的余弦值．
【答案】（1）见解析（2）
【解析】
（1）通过勾股定理得出
，又
，进而可得
平面
，则可得到
，问题得证；
（2）如图，以
为原点，
，
，
所在直线分别为
轴，
轴，
轴，求出平面
的法向量和平面
的法向量，利用空间向量的夹角公式可得答案.
（1）因为
平面
，所以，
又因为
，
，
，所以
，
因此
，所以，
因此平面，所以
，
从而，又四边形
为平行四边形，
则四边形为矩形；
（2）如图，以为原点，，，所在直线分别为轴，轴，轴，所以
，
平面的法向量
，设平面的法向量
，
由
，
由
，
令
，即
，
所以，
，
所以，所求二面角的余弦值是.
练习册系列答案
学业测评一课一测系列答案
相关题目
【题目】为了调查一款手机的使用时间，研究人员对该款手机进行了相应的测试，将得到的数据统计如下图所示：
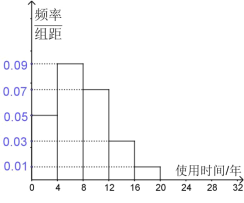
并对不同年龄层的市民对这款手机的购买意愿作出调查，得到的数据如下表所示：
愿意购买该款手机 | 不愿意购买该款手机 | 总计 | |
40岁以下 | 600 | ||
40岁以上 | 800 | 1000 | |
总计 | 1200 |
（1）根据图中的数据，试估计该款手机的平均使用时间；
（2）请将表格中的数据补充完整，并根据表中数据，判断是否有99．9％的把握认为“愿意购买该款手机”与“市民的年龄”有关．
参考公式：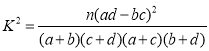
，其中
．
参考数据：
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
