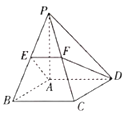
题目内容
【题目】已知点
是抛物线
：
的焦点，点
为抛物线的对称轴与其准线的交点，过作抛物线的切线，切点为
，若点恰好在以，为焦点的双曲线上，则双曲线的离心率为（ ）
A. 
B. 
C. 
D. 
【答案】D
【解析】
根据抛物线的性质，设出直线方程，代入抛物线方程，求得k的值，设出双曲线方程，求得2a＝丨AF2丨﹣丨AF1丨＝（
1）p，利用双曲线的离心率公式求得e．
直线F2A的直线方程为：y＝kx
，F1（0，
），F2（0，），
代入抛物线C：x2＝2py方程，整理得：x2﹣2pkx+p2＝0，
∴△＝4k2p2﹣4p2＝0，解得：k＝±1，
∴A（p，），设双曲线方程为：
1，
丨AF1丨＝p，丨AF2丨
p，
2a＝丨AF2丨﹣丨AF1丨＝（ 1）p，
2c＝p，
∴离心率e
1，
故选：D．
备战中考寒假系列答案
【题目】我市某区2018年房地产价格因“棚户区改造”实行货币化补偿，使房价快速走高，为抑制房价过快上涨，政府从2019年2月开始采用实物补偿方式（以房换房），3月份开始房价得到很好的抑制，房价渐渐回落，以下是2019年2月后该区新建住宅销售均价的数据：
月份 | 3 | 4 | 5 | 6 | 7 |
价格 | 83 | 82 | 80 | 78 | 77 |
（1）研究发现，3月至7月的各月均价
（百元/平方米）与月份
之间具有较强的线性相关关系，求价格（百元/平方米）关于月份的线性回归方程；
（2）用
表示用（1）中所求的线性回归方程得到的与
对应的销售均价的估计值，3月份至7月份销售均价估计值与实际相应月份销售均价
差的绝对值记为
，即
，
.若
，则将销售均价的数据
参考公式：回归方程系数公式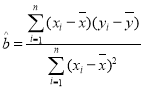
，
；参考数据：
，
.
【题目】某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验，并获得了煤气开关旋钮旋转的弧度数
与烧开一壶水所用时间
的一组数据，且作了一定的数据处理（如下表），得到了散点图（如下图）.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中
，
.
（1）根据散点图判断，
与
哪一个更适宜作烧水时间关于开关旋钮旋转的弧度数的回归方程类型？（不必说明理由）
（2）根据判断结果和表中数据，建立关于的回归方程；
（3）若单位时间内煤气输出量
与旋转的弧度数成正比，那么，利用第（2）问求得的回归方程知为多少时，烧开一壶水最省煤气？
附：对于一组数据
，其回归直线
的斜率和截距的最小二乘法估计值分别为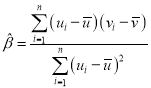
，
