题目内容
【题目】在△ABC中,角A、B、C所对的边分别为a,b,c,满足(2a﹣c)cosB=bcosC. 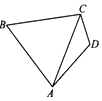
(1)求B的大小;
(2)如图,AB=AC,在直线AC的右侧取点D,使得AD=2CD=4.当角D为何值时,四边形ABCD面积最大.
【答案】
(1)解:∵(2a﹣c)cosB=bcosC,
∴(2sinA﹣sinC)cosB=sinBcosC,
∴2sinAcosB﹣sinCcosB=sinBcosC,
∴2sinAcosB=sin(B+C)=sinA,
∵sinA≠0,
∴cosB= ![]() ,
,
∴B= ![]()
(2)解:∵AB=AC,B= ![]() ,
,
∴△ABC为等边三角形,
∵若四边形ABCD面积最大,
∴△ADC的面积最大,
设AC=x,在△ADC中,由余弦定理可得x2=AC2=CD2+AD2﹣2CDADcosD=4+16﹣2×2×4cosD,
∴cosD= ![]() ,
,
∴sinD= ![]() ,当x2=20时,即x=2
,当x2=20时,即x=2 ![]() ,﹣(20﹣x2)2+162最大,即sinD最大,最大为1,
,﹣(20﹣x2)2+162最大,即sinD最大,最大为1,
∵S△ADC= ![]() CDADsinD=4sinD,
CDADsinD=4sinD,
∴D= ![]() 时,S△ADC的面积最大,
时,S△ADC的面积最大,
∴当D= ![]() 时,四边形ABCD面积最大
时,四边形ABCD面积最大
【解析】(1)根据正弦定理和两角和的正弦公式即可求出B的大小,(2)若四边形ABCD面积最大,则△ADC的面积最大,根据余弦定理和同角的三角函数的关系以及二次函数的性质可得当D= ![]() 时,四边形ABCD面积最大
时,四边形ABCD面积最大

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目

