Question

【题目】已知F为抛物线C：x2=2py（p＞0）的焦点，过F的直线l与C交于A，B两点，M为AB中点，点M到x轴的距离为d，|AB|=2d+1．
（1）求p的值；
（2）过A，B分别作C的两条切线l1 ， l2 ， l1∩l2=N．请选择x，y轴中的一条，比较M，N到该轴的距离．

Answer 1

【答案】
（1）解：设抛物线C的准线为m，如图，过A，B，M分别作直线m的垂线，垂足分别为A1，B1，M1．

，

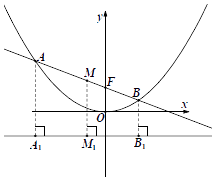
所以 ，所以p=1

（2）解：由（1）得，抛物线 ，

因为直线l不垂直于x轴，可设 ．

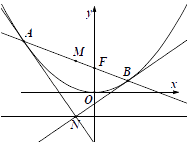
由 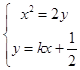，消去y得，x2﹣2kx﹣1=0，

由韦达定理得， ，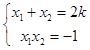

所以 ．

抛物线C：x2=2y，即 ，故y'=x，

因此，切线l1的斜率为x1，切线l1的方程为y=x1（x﹣x1）+y1，

整理得 ①，

同理可得 ②，

联立①②并消去y，得 ，

把 代入①，得 ，故 ．

因为xM=xN， ，

所以M，N到y轴的距离相等；M到x轴的距离不小于N到x轴的距离．

（注：只需比较M，N到x轴或y轴的距离中的一个即可）

【解析】（1）利用抛物线的定义，建立方程，即可得出结论；（2）判断xM=xN， ，即可得出结论．