题目内容
【题目】在△ABC中，角A，B，C所对的边分别为a，b，c，且 
．
（1）求A的大小；
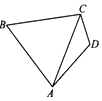
（2）若 
，D是BC的中点，求AD的长．
【答案】
（1）解：由正弦定理，得： 
，
即 
，
由余弦定理可得：cosA= 
= 
=﹣ 
∵0＜A＜π，
∴A= 
（2）解：将 
，代入a2=b2+c2+ 
bc，可得：c2+6c﹣72=0，
因为c＞0，所以c=6
又∵ 
= 
（ 
），
∴| |2= 
（ ）2= （c2+2cbcosA+b2）= 
，
所以 
【解析】（1）由正弦定理，得 
，结合余弦定理可得：cosA=﹣ 
，结合范围0＜A＜π，即可得解A的值．（2）由已知及（1）利用余弦定理可求c的值，又 
= 
（ 
），平方后即可得解AD的值．
【考点精析】认真审题，首先需要了解正弦定理的定义(正弦定理:
)．
练习册系列答案
相关题目
