Question

【题目】在平面直角坐标系xOy中，直线l的参数方程为 （t为参数），其中0≤α＜π．在以O为极点，x轴的正半轴为极轴的极坐标系中，曲线C1：ρ=4cosθ．直线l与曲线C1相切．
（1）将曲线C1的极坐标方程化为直角坐标方程，并求α的值．
（2）已知点Q（2，0），直线l与曲线C2：x2+ =1交于A，B两点，求△ABQ的面积．

Answer 1

【答案】
（1）解：曲线C1：ρ=4cosθ，即ρ2=4ρcosθ，化为直角坐标方程：x2+y2=4x，配方为C1：（x﹣2）2+y2=4，可得圆心（2，0），半径r=2

直线l的参数方程为 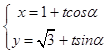（t为参数），其中0≤α＜π，普通方程为y﹣ =k（x﹣1），k=tanα，0≤α＜π，

∵直线l与曲线C1相切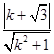，∴ =2，∴k= ，∴α=

（2）解：直线l的方程为y= x+ ，代入曲线C2：x2+ =1，整理可得10x2+4x﹣5=0，

∴|AB|= = ，

Q到直线的距离d= 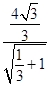=2，

∴△ABQ的面积S= =

【解析】（1）曲线C1：ρ=4cosθ，即ρ2=4ρcosθ，把ρ2=x2+y2，x=ρcosθ代入可得C的直角坐标方程，利用直线l与曲线C1相切求α的值．（2）直线l的方程为y= x+ ，代入曲线C2：x2+ =1，整理可得10x2+4x﹣5=0，求出|AB|，Q到直线的距离，即可求△ABQ的面积．