题目内容
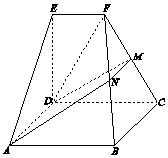
【题目】如图,在几何体ABCDEF中,底面ABCD为矩形,EF∥CD,CD⊥EA,CD=2EF=2,ED= ![]() .M为棱FC上一点,平面ADM与棱FB交于点N.
.M为棱FC上一点,平面ADM与棱FB交于点N. 
(Ⅰ)求证:ED⊥CD;
(Ⅱ)求证:AD∥MN;
(Ⅲ)若AD⊥ED,试问平面BCF是否可能与平面ADMN垂直?若能,求出 ![]() 的值;若不能,说明理由.
的值;若不能,说明理由.
【答案】(Ⅰ)证明:因为ABCD为矩形,所以VD⊥AD.
又因为CD⊥EA,
所以CD⊥平面EAD.
所以ED⊥CD.
(Ⅱ)证明:因为ABCD为矩形,所以AD∥BC,
所以AD∥平面FBC.
又因为平面ADMN∩平面FBC=MN,
所以AD∥MN
(Ⅲ)解:平面ADMN与平面BCF可以垂直.证明如下:
连接DF.
因为AD⊥ED,AD⊥CD.ED∩CD=D,
所以AD⊥平面CDEF.
所以AD⊥DM.
因为AD∥MN,所以DM⊥MN.
因为平面ADMN∩平面FBC=MN,
若使平面ADMN⊥平面BCF,
则DM⊥平面BCF,所以DM⊥FC.
在梯形CDEF中,因为EF∥CD,DE⊥CD,CD=2EF=2,ED= ![]() ,
,
所以DF=DC=2.
所以若使DM⊥FC能成立,则M为FC的中点.
所以 ![]() =
= ![]() .
.
【解析】(Ⅰ)证明:CD⊥平面EAD,即可证明ED⊥CD;(Ⅱ)证明AD∥平面FBC,即可证明:AD∥MN;(Ⅲ)若使平面ADMN⊥平面BCF,则DM⊥平面BCF,所以DM⊥FC,可得DF=DC=2.若使DM⊥FC能成立,则M为FC的中点.
【考点精析】认真审题,首先需要了解直线与平面垂直的判定(一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想),还要掌握直线与平面垂直的性质(垂直于同一个平面的两条直线平行)的相关知识才是答题的关键.

【题目】已知抛物线C:y2=4x的焦点为F,准线为l,P为C上一点,PQ垂直l于点Q,M,N分别为PQ,PF的中点,MN与x轴相交于点R,若∠NRF=60°,则|FR|等于( )
A.![]()
B.1
C.2
D.4
【题目】某大学为调研学生在A,B两家餐厅用餐的满意度,从在A,B两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.整理评分数据,将分数以10为组距分成6组:[0,10),[10,20),[20,30),[30,40),[40,50),[50,60],得到A餐厅分数的频率分布直方图,和B餐厅分数的频数分布表:
B餐厅分数频数分布表 | |
分数区间 | 频数 |
[0,10) | 2 |
[10,20) | 3 |
[20,30) | 5 |
[30,40) | 15 |
[40,50) | 40 |
[50,60] | 35 |
定义学生对餐厅评价的“满意度指数”如下:
分数 | [0,30) | [30,50) | [50,60] |
满意度指数 | 0 | 1 | 2 |

(Ⅰ)在抽样的100人中,求对A餐厅评价“满意度指数”为0的人数;
(Ⅱ)从该校在A,B两家餐厅都用过餐的学生中随机抽取1人进行调查,试估计其对A餐厅评价的“满意度指数”比对B餐厅评价的“满意度指数”高的概率;
(Ⅲ)如果从A,B两家餐厅中选择一家用餐,你会选择哪一家?说明理由.