题目内容
20.已知圆C的极坐标方程是ρ=4sinθ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是$\left\{\begin{array}{l}{x=\frac{\sqrt{3}}{2}t}\\{y=\frac{1}{2}t+m}\end{array}\right.$(t是参数).若直线l与圆C相切,求正数m的值.分析 由x=ρcosθ,y=ρsinθ,ρ2=x2+y2,化简圆C的方程为普通方程,运用代入法求得直线的普通方程,再由直线和圆相切的条件d=r,解方程可得m.
解答 解:由ρ=4sinθ,得ρ2=4ρsinθ,所以x2+y2-4y=0,
即圆C方程为x2+(y-2)2=4.其圆心为(0,2),半径为2.
又由$\left\{\begin{array}{l}{x=\frac{\sqrt{3}}{2}t}\\{y=\frac{1}{2}t+m}\end{array}\right.$(t是参数).消t得x-$\sqrt{3}$y+$\sqrt{3}$m=0,
因为直线l与圆C相切,所以$\frac{|-2\sqrt{3}+\sqrt{3}m|}{2}$=2,得m=2±$\frac{4\sqrt{3}}{3}$,
又m>0,所以m=2+$\frac{4\sqrt{3}}{3}$.
点评 本题考查极坐标方程和参数方程与普通方程的互化,主要考查直线和圆的位置关系:相切的条件,属于中档题.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
11.已知随机变量ξ服从正态分布N(2,1),若P(ξ>3)=0.023,则P(1≤ξ≤3)=( )
| A. | 0.046 | B. | 0.623 | C. | 0.977 | D. | 0.954 |
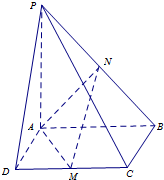 如图4,已知四棱锥P-ABCD,底面ABCD是正方形,PA⊥面ABCD,点M是CD的中点,点N是PB的中点,连接AM,AN,MN.
如图4,已知四棱锥P-ABCD,底面ABCD是正方形,PA⊥面ABCD,点M是CD的中点,点N是PB的中点,连接AM,AN,MN.