Question

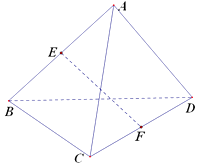
【题目】将半径都为1的4个钢球完全装入形状为正四面体的容器里，这个正四面体的高的最小值为（ ）
A.
B.2+
C.4+
D.

Answer 1

【答案】C
【解析】解：由题意知，底面放三个钢球，上再落一个钢球时体积最小． 于是把钢球的球心连接，则又可得到一个棱长为2的小正四面体，则不难求出这个小正四面体的高为 ，
且由正四面体的性质可知：正四面体的中心到底面的距离是高的 ，且小正四面体的中心和正四面体容器的中心应该是重合的，
∴小正四面体的中心到底面的距离是 × = ，正四面体的中心到底面的距离是 +1 （1即小钢球的半径），
所以可知正四棱锥的高的最小值为 （ +1）×4=4+ ，
故选 C．
【考点精析】掌握棱锥的结构特征是解答本题的根本，需要知道侧面、对角面都是三角形；平行于底面的截面与底面相似，其相似比等于顶点到截面距离与高的比的平方．