题目内容
【题目】各项均为正数的等比数列![]() 满足
满足![]() ,
, ![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若 ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)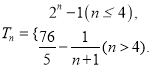
【解析】试题分析:(1)通过![]() ,
, ![]() 及数列
及数列![]() 的各项均为正数,可得
的各项均为正数,可得![]() ,计算即可;(2)
,计算即可;(2)![]() 时;利用分组求和与等比数列求和,
时;利用分组求和与等比数列求和, ![]() 通过
通过![]()
![]()
![]() ,可得
,可得![]()
![]() ,利用错位相减法及等比数列的求和公式计算即可.
,利用错位相减法及等比数列的求和公式计算即可.
试题解析:(Ⅰ)设等比数列![]() 的公比为
的公比为![]() ,由
,由![]() 得
得
由![]() ,得
,得![]() 或
或![]() ,
,
![]() 数列
数列![]() 为正项数列,
为正项数列, ![]() ,
,
代入①,得![]() ,
, ![]() .
.
(Ⅱ)由(Ⅰ)知当![]() 时,
时, ![]()
![]()
![]() ,
,
此时![]()
![]() ,
,
当![]() 时,
时, ![]()
![]()
![]()
![]() .
.
当![]() 时,
时,
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
综上可知,数列![]() 的前
的前![]() 项和
项和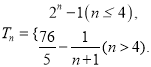
【方法点晴】裂项相消法是最难把握的求和方法之一,其原因是有时很难找到裂项的方向,突破这一难点的方法是根据式子的结构特点,掌握一些常见的裂项技巧:①![]() ;②
;②![]()
![]() ;③
;③![]() ;
;
④ ;此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.
;此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
【题目】某高校在2014年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下表所示.
组号 | 分组 | 频数 | 频率 |
第1组 | [160,165) | 5 | 0.050 |
第2组 | [165,170) | n | 0.350 |
第3组 | [170,175) | 30 | p |
第4组 | [175,180) | 20 | 0.200 |
第5组 | [180,185] | 10 | 0.100 |
合计 | 100 | 1.000 |
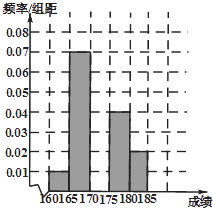
(1)求频率分布表中n,p的值,并补充完整相应的频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样的方法抽取6名学生进入第二轮面试,则第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定从6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有1名学生被甲考官面试的概率.
