题目内容
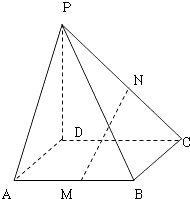
【题目】如图四棱锥P﹣ABCD中，平面PAD⊥平面ABCD，AB∥CD，∠ABC=90°，且CD=2，AB=BC=PA=1，PD= 
． 
（1）求三棱锥A﹣PCD的体积；
（2）问：棱PB上是否存在点E，使得PD∥平面ACE？若存在，求出 
的值，并加以证明；若不存在，请说明理由．
【答案】
（1）解：取CD中点G，连接AG，
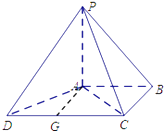
∵CD=2AB，AB∥CD，
∴AB∥GC，AB=GC，
∴四边形AGCB为平行四边形，
∴∠AGD=∠DCB=∠ABC=90°，
在Rt△AGD中，∵AG=BC=1，DG= 
CD=1，
∴AD= 
= 
，
∴PD2=3=PA2+AD2，
∴∠PAD=90°，即PA⊥AD，
∵平面PAD⊥平面ABCD，平面PAD∩平面ABCD=AD，
∴PA⊥平面ABCD，
∵S△ACD= 
=1，
∴VA﹣PCD=VP﹣ACD= 
= 
= 
．
（2）解：棱PB上存在点E，当 
= 时，PD∥平面ACE．
证明：连接BD交AC于点O，连接OE．
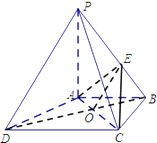
∵AB∥CD，CD=2AB，
∴ 
= 
= ，
∴ 
= ，又 
，
∴ 
，
∴OE∥DP，
又OE平面ACE，PDACE，
∴PD∥ACE．
【解析】（1）取CD中点G，连接AG，利用已知可得：四边形AGCB为平行四边形，∠AGD=∠DCB=∠ABC=90°，在Rt△AGD中，AG=BC=1，DG= CD=1，利用勾股定理与逆定理可得：PA⊥AD．利用面面垂直的性质定理可得：PA⊥平面ABCD，利用VA﹣PCD=VP﹣ACD= ，即可得出．（2）棱PB上存在点E，当 = 时，PD∥平面ACE．连接BD交AC于点O，连接OE．利用平行线分线段成比例定理再三角形中的应用：可得OE∥DP．
【考点精析】认真审题，首先需要了解直线与平面平行的判定(平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行)．
