题目内容
【题目】若正项数列{an}满足: ![]() =an+1﹣an(a∈N*),则称此数列为“比差等数列”.
=an+1﹣an(a∈N*),则称此数列为“比差等数列”.
(1)请写出一个“比差等数列”的前3项的值;
(2)设数列{an}是一个“比差等数列”
(i)求证:a2≥4;
(ii)记数列{an}的前n项和为Sn , 求证:对于任意n∈N*,都有Sn> ![]() .
.
【答案】
(1)解:解:一个“比差等数列”的前3项可以是:2,4, ![]()
(2)解:(i)证明:当n=1时, ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
∵an>0,∴ ![]() ,则a1﹣1>0,即a1>1,
,则a1﹣1>0,即a1>1,
∴ ![]() ≥2
≥2 ![]() +2=4,
+2=4,
当且仅当 ![]() 时取等号,
时取等号,
则a2≥4成立;
(ii)由an>0得,an+1﹣an= ![]() ≥0,
≥0,
∴an+1≥an>0,则an+1﹣an= ![]() ,
,
由a2≥4得,a3﹣a2≥1,a4﹣a3≥1,…,an﹣an﹣1≥1,
以上 n﹣1个不等式相加得,an≥(n﹣2)+4=n+2(n≥2),
当n≥2时,Sn=a1+a2+a3+…+an
≥1+4+(3+2)+…+(n+2)≥(1+2)+(2+2)+…+(n+2)﹣2
= ![]() ﹣2=
﹣2= ![]() ,
,
当n=1时,由(i)知S1=a1>1≥ ![]() ,
,
综上可得,对于任意n∈N*,都有Sn> ![]()
【解析】(1)根据“比差等数列”的定义,写出一个“比差等数列”的前3项即可;(2)(i)当n=1时可得 ![]() ,求出a2利用分离常数法化简,由an>0可得a1>1,利用基本不等式证明a2≥4;(ii)由an>0得an+1﹣an=
,求出a2利用分离常数法化简,由an>0可得a1>1,利用基本不等式证明a2≥4;(ii)由an>0得an+1﹣an= ![]() ≥0,得an+1≥an>0从而得到an+1﹣an=
≥0,得an+1≥an>0从而得到an+1﹣an= ![]() ,列出n﹣1个不等式并相加得an≥n+2(n≥2),当n≥2时利用放缩法和等差数列的前n项和公式化简后,得到Sn的不等式再验证n=1时是否成立即可.
,列出n﹣1个不等式并相加得an≥n+2(n≥2),当n≥2时利用放缩法和等差数列的前n项和公式化简后,得到Sn的不等式再验证n=1时是否成立即可.
【考点精析】通过灵活运用数列的前n项和和数列的通项公式,掌握数列{an}的前n项和sn与通项an的关系 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】雾霾天气是一种大气污染状态,PM2.5被认为是造成雾霾天气的“元凶”,PM2.5日均值越小,空气质量越好.国家环境标准设定的PM2.5日均值(微克/立方米)与空气质量等级对应关系如表:
PM2.5日均值 | 0﹣﹣35 | 35﹣﹣75 | 75﹣﹣115 | 115﹣﹣150 | 150﹣﹣250 | 250以上 |
空气质量等级 | 1级 | 2级 | 3级 | 4级 | 5级 | 6级 |
由某市城市环境监测网获得4月份某5天甲、乙两城市的空气质量指数数据,用茎叶图表示,如图所示.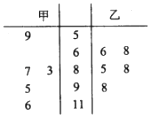
(1)试根据统计数据,分别写出两城区的PM2.5日均值的中位数,并从中位数角度判断哪个城区的空气质量较好?
(2)考虑用频率估计概率的方法,试根据统计数据,估计甲城区某一天空气质量等级为3
(3)分别从甲、乙两个城区的统计数据中任取一个,试求这两城区空气质量等级相同的概率.