Question

【题目】如图，有一壁画，最高点A处离地面AO=4m，最低点B处离地面BO=2m，观赏它的C点在过墙角O点与地面成30°角的射线上．

（1）设点C到墙的距离为x，当x= m时，求tanθ的值；
（2）问C点离墙多远时，视角θ最大？

Answer 1

【答案】
（1）解：作CD⊥AO于D，则 ，

在直角△CDO中， ，

， ，

因∠BCD，∠ACD都为锐角，所以∠BCD=30°，∠ACD=60°，

所以

（2）解：设∠BCD=α，∠ACD=β．作如下规定：

当D点在B点下方时α为正，当D点在B点上方时α为负，当D点与B重合时α为零．类似地β也如此规定．

于是有 ，θ=β﹣α，

，

= =

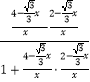当且仅当 ， 时tanθ最大，从而θ最大，此时C点离墙 ．

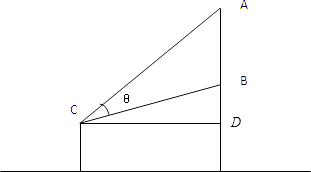
【解析】（1）过C作CD⊥AO，垂足为D，则θ=∠ACD﹣∠BCD，利用差角的正切公式，求tanθ的值；（2）利用差角的正切公式，我们可以求得tanθ，利用基本不等式可得结论．