题目内容
【题目】已知一个几何体的三视图如图所示. 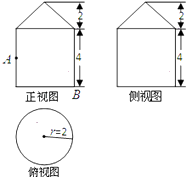
(1)求此几何体的表面积;
(2)在如图的正视图中,如果点A为所在线段中点,点B为顶点,求在几何体侧面上从点A到点B的最短路径的长.
【答案】
(1)解:由三视图知:几何体是一个圆锥与一个圆柱的组合体,且圆锥与圆柱的底面半径为2,母线长分别为2 ![]() 、4,
、4,
其表面积是圆锥的侧面积、圆柱的侧面积和圆柱的一个底面积之和.
S圆锥侧= ![]() ×2π×2×2
×2π×2×2 ![]() =4
=4 ![]() π;
π;
S圆柱侧=2π×2×4=16π;
S圆柱底=π×22=4π.
∴几何体的表面积S=20π+4 ![]() π;
π;
(2)解:沿A点与B点所在母线剪开圆柱侧面,如图:
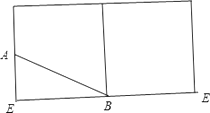
则AB= ![]() =
= ![]() =2
=2 ![]() ,
,
∴以从A点到B点在侧面上的最短路径的长为2 ![]() .
.
【解析】(1)几何体是一个圆锥与一个圆柱的组合体,由三视图判断圆锥与圆柱的底面半径与母线长,根据其表面积是圆锥的侧面积、圆柱的侧面积和圆柱的一个底面积之和,代入公式计算;(2)利用圆柱的侧面展开图,求得EB的长,再利用勾股定理求AB的圆柱面距离.
【考点精析】本题主要考查了由三视图求面积、体积的相关知识点,需要掌握求体积的关键是求出底面积和高;求全面积的关键是求出各个侧面的面积才能正确解答此题.

练习册系列答案
相关题目