题目内容
已知不过坐标原点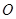 的直线
的直线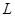 与抛物线
与抛物线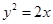 相交于
相交于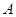 、
、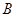 两点,且
两点,且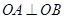 ,
,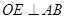 于
于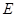 .
.
①求证:直线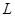 过定点;
过定点;
②求点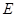 的轨迹方程.
的轨迹方程.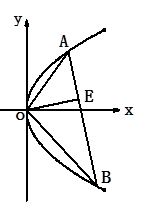
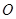 的直线
的直线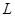 与抛物线
与抛物线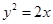 相交于
相交于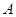 、
、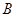 两点,且
两点,且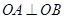 ,
,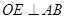 于
于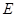 .
.①求证:直线
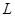 过定点;
过定点; ②求点
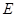 的轨迹方程.
的轨迹方程.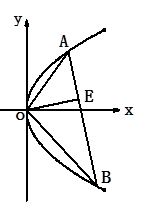
(1)见解析;(2)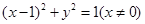 .
.
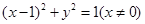 .
.(1)为避免对斜率不存在情况的讨论,可以设直线方程为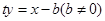 ,然后根据题目给的方程条件
,然后根据题目给的方程条件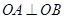 ,即可确定b的值或找到b与t的关系,进而确定定点.
,即可确定b的值或找到b与t的关系,进而确定定点.
(2)由于第一问确定了定点C(2,0),然后可知点E在以OC为直径的圆上.求出此圆的方程即可.
也要利用交轨法求其轨迹方程.
解:令直线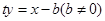 与抛物线
与抛物线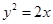 相交于
相交于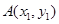 、
、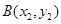 两点
两点
(给直线方程给分) ……………………1分
 ……………………2分
……………………2分
于是,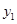 、
、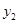 是此方程的两实根,由韦达定理得:
是此方程的两实根,由韦达定理得:
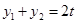
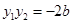 ……………………3分
……………………3分
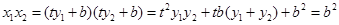 …………4分
…………4分
又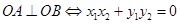 ……………………5分
……………………5分
∴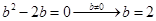 ……………………6分
……………………6分
故直线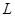 :
: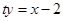 过定点
过定点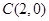 ……………………8分
……………………8分
②∵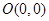 ,
,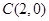 ,
,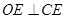 ……………………9分
……………………9分
∴点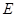 的轨迹是以线段
的轨迹是以线段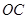 为直径的圆除去点
为直径的圆除去点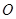 , ……………………11分
, ……………………11分
故点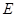 的轨迹方程为
的轨迹方程为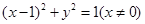 ……………………12分
……………………12分
说明:直线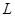 的方程设为
的方程设为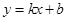 又没有讨论
又没有讨论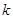 不存在的情况扣2分;轨迹方程中没有限制
不存在的情况扣2分;轨迹方程中没有限制 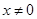 扣1分.
扣1分.
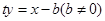 ,然后根据题目给的方程条件
,然后根据题目给的方程条件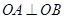 ,即可确定b的值或找到b与t的关系,进而确定定点.
,即可确定b的值或找到b与t的关系,进而确定定点.(2)由于第一问确定了定点C(2,0),然后可知点E在以OC为直径的圆上.求出此圆的方程即可.
也要利用交轨法求其轨迹方程.
解:令直线
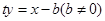 与抛物线
与抛物线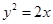 相交于
相交于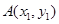 、
、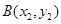 两点
两点(给直线方程给分) ……………………1分
 ……………………2分
……………………2分于是,
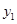 、
、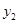 是此方程的两实根,由韦达定理得:
是此方程的两实根,由韦达定理得: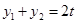
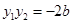 ……………………3分
……………………3分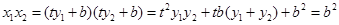 …………4分
…………4分又
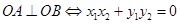 ……………………5分
……………………5分∴
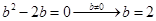 ……………………6分
……………………6分故直线
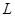 :
: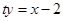 过定点
过定点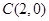 ……………………8分
……………………8分②∵
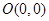 ,
,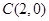 ,
,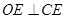 ……………………9分
……………………9分∴点
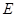 的轨迹是以线段
的轨迹是以线段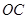 为直径的圆除去点
为直径的圆除去点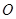 , ……………………11分
, ……………………11分故点
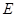 的轨迹方程为
的轨迹方程为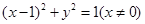 ……………………12分
……………………12分说明:直线
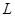 的方程设为
的方程设为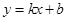 又没有讨论
又没有讨论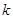 不存在的情况扣2分;轨迹方程中没有限制
不存在的情况扣2分;轨迹方程中没有限制 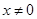 扣1分.
扣1分.
练习册系列答案
相关题目
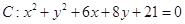 ,抛物线
,抛物线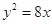 的准线为
的准线为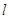 ,设抛物线上任意一点
,设抛物线上任意一点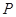 到直线
到直线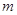 ,则
,则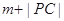 的最小值为
的最小值为 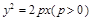 焦点的直线与抛物线交于
焦点的直线与抛物线交于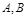 两点,
两点,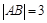 ,且AB中点的纵坐标为
,且AB中点的纵坐标为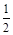 ,则
,则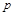 的值为 .
的值为 .
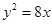 的焦点为
的焦点为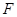 ,准线为
,准线为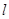 ,
,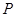 为抛物线上一点,
为抛物线上一点,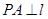 ,
,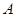 为垂足.如果直线
为垂足.如果直线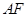 的斜率为
的斜率为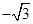 ,那么
,那么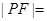
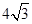
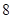
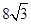
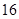
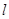 与抛物线
与抛物线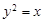 交于
交于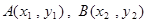 两点,与
两点,与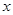 轴相交于点
轴相交于点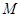 ,且
,且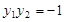 .
.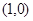 ;
;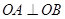 ;
;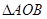 的面积的最小值.
的面积的最小值.
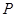 是抛物线
是抛物线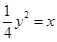 上一个动点,则点
上一个动点,则点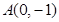 的距离与点
的距离与点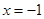 的距离和的最小值是 。
的距离和的最小值是 。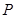 为抛物线
为抛物线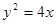 上一个动点,
上一个动点,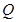 为圆
为圆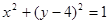 上一个动点,那么点
上一个动点,那么点
 过抛物线
过抛物线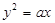 的焦点F,且与
的焦点F,且与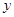 轴相交于点A,若
轴相交于点A,若