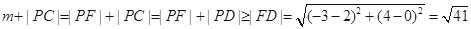题目内容
已知圆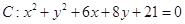 ,抛物线
,抛物线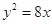 的准线为
的准线为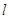 ,设抛物线上任意一点
,设抛物线上任意一点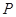 到直线
到直线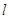 的距离为
的距离为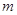 ,则
,则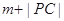 的最小值为
的最小值为
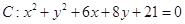 ,抛物线
,抛物线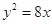 的准线为
的准线为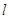 ,设抛物线上任意一点
,设抛物线上任意一点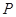 到直线
到直线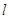 的距离为
的距离为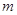 ,则
,则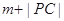 的最小值为
的最小值为 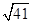
由于圆C的方程为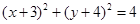 , 抛物线的准线方程为
, 抛物线的准线方程为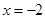 ,
,
圆C关于x轴的对称圆D的方程为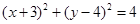 ,根据抛物线的定义
,根据抛物线的定义
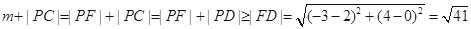
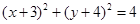 , 抛物线的准线方程为
, 抛物线的准线方程为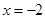 ,
,圆C关于x轴的对称圆D的方程为
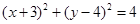 ,根据抛物线的定义
,根据抛物线的定义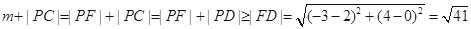

练习册系列答案
相关题目
题目内容
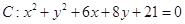 ,抛物线
,抛物线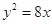 的准线为
的准线为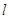 ,设抛物线上任意一点
,设抛物线上任意一点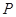 到直线
到直线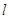 的距离为
的距离为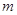 ,则
,则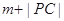 的最小值为
的最小值为 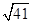
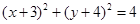 , 抛物线的准线方程为
, 抛物线的准线方程为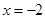 ,
,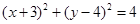 ,根据抛物线的定义
,根据抛物线的定义