题目内容
如图,直线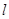 与抛物线
与抛物线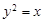 交于
交于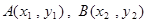 两点,与
两点,与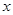 轴相交于点
轴相交于点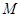 ,且
,且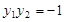 .
.
(1)求证: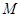 点的坐标为
点的坐标为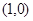 ;
;
(2)求证: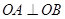 ;
;
(3)求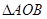 的面积的最小值.
的面积的最小值.
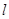 与抛物线
与抛物线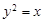 交于
交于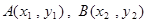 两点,与
两点,与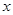 轴相交于点
轴相交于点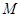 ,且
,且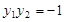 .
.(1)求证:
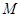 点的坐标为
点的坐标为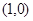 ;
;(2)求证:
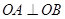 ;
;(3)求
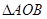 的面积的最小值.
的面积的最小值.
(1 ) 设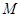 点的坐标为
点的坐标为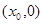 , 直线
, 直线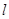 方程为
方程为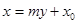 , 代入
, 代入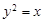 得
得
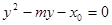 ①
① 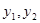 是此方程的两根,
是此方程的两根,
∴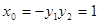 ,即
,即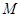 点的坐标为(1, 0).
点的坐标为(1, 0).
(2 ) ∵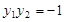 ∴
∴ 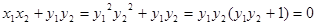
∴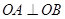 .
.
(3)由方程①,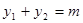 ,
, 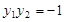 , 且
, 且 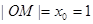 ,
,
于是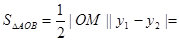
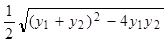 =
=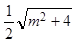 ≥1,
≥1,
∴ 当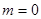 时,
时,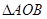 的面积取最小值1.
的面积取最小值1.
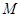 点的坐标为
点的坐标为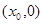 , 直线
, 直线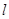 方程为
方程为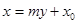 , 代入
, 代入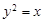 得
得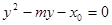 ①
① 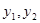 是此方程的两根,
是此方程的两根,∴
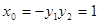 ,即
,即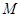 点的坐标为(1, 0).
点的坐标为(1, 0).(2 ) ∵
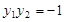 ∴
∴ 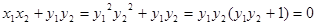
∴
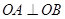 .
.(3)由方程①,
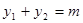 ,
, 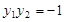 , 且
, 且 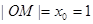 ,
,于是
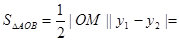
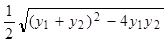 =
=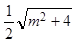 ≥1,
≥1,∴ 当
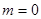 时,
时,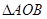 的面积取最小值1.
的面积取最小值1.设出点M的坐标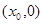 ,并把过点M的方程设出来.为避免对斜率不存在的情况进行讨论,可以设其方程为
,并把过点M的方程设出来.为避免对斜率不存在的情况进行讨论,可以设其方程为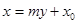 ,然后与抛物线方程联立消x,根据
,然后与抛物线方程联立消x,根据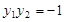 ,即可建立关于
,即可建立关于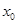 的方程.求出
的方程.求出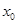 的值.
的值.
(2)在第(1)问的基础上,证明: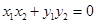 即可.
即可.
(3)先建立面积S关于m的函数关系式,根据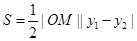 建立即可,然后再考虑利用函数求最值的方法求最值.
建立即可,然后再考虑利用函数求最值的方法求最值.
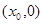 ,并把过点M的方程设出来.为避免对斜率不存在的情况进行讨论,可以设其方程为
,并把过点M的方程设出来.为避免对斜率不存在的情况进行讨论,可以设其方程为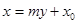 ,然后与抛物线方程联立消x,根据
,然后与抛物线方程联立消x,根据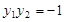 ,即可建立关于
,即可建立关于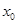 的方程.求出
的方程.求出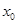 的值.
的值.(2)在第(1)问的基础上,证明:
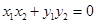 即可.
即可.(3)先建立面积S关于m的函数关系式,根据
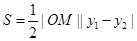 建立即可,然后再考虑利用函数求最值的方法求最值.
建立即可,然后再考虑利用函数求最值的方法求最值.
练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
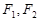 分别为椭圆
分别为椭圆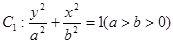 的上下焦点,其中
的上下焦点,其中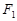 也是抛物线
也是抛物线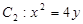 的焦点,点
的焦点,点 是
是 与
与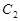 在第二象限的交点,且
在第二象限的交点,且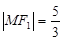 .
.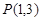 和圆
和圆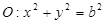 ,过点
,过点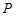 的动直线
的动直线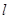 与圆
与圆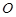 相交于不同的两
相交于不同的两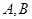 ,在线段
,在线段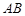 上取一点
上取一点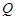 ,满足
,满足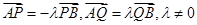 且
且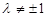 .
.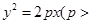

 的对称轴上的定点
的对称轴上的定点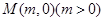 ,作直线
,作直线 与抛物线相交于
与抛物线相交于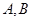 两点.
两点.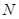 是定直线
是定直线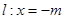 上的任一点,试探索三条直线
上的任一点,试探索三条直线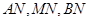 的斜率之间的关系,并给出证明.
的斜率之间的关系,并给出证明.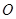 的直线
的直线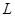 与抛物线
与抛物线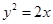 相交于
相交于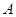 、
、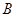 两点,且
两点,且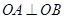 ,
,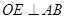 于
于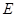 .
.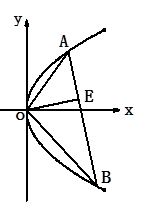
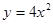 的焦点为圆心,与其准线相切的圆方程是( )
的焦点为圆心,与其准线相切的圆方程是( )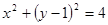
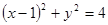
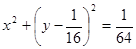
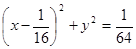
 为过抛物线
为过抛物线 焦点
焦点 的一条弦,设
的一条弦,设 ,以下结论正确的是____________________,
,以下结论正确的是____________________, 且
且 ②
② 的最小值为
的最小值为 ③以
③以 为直径的圆与
为直径的圆与 轴相切;
轴相切; 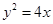 只有一个公共点,则k的值是 。
只有一个公共点,则k的值是 。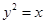 和
和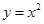 所围成的图形的面积为______________
所围成的图形的面积为______________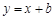 交抛物线
交抛物线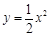 于
于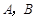 两点,
两点, 为抛物线顶点,
为抛物线顶点,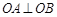 ,则
,则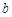 的值为( )
的值为( )