题目内容
(本小题满分10分)选修4-5:不等式选讲
已知函数 .
.
(1)当 时,求函数
时,求函数 的定义域;
的定义域;
(2)若关于 的不等式
的不等式 的解集是
的解集是 ,求
,求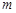 的取值范围.
的取值范围.
已知函数
 .
. (1)当
 时,求函数
时,求函数 的定义域;
的定义域;(2)若关于
 的不等式
的不等式 的解集是
的解集是 ,求
,求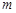 的取值范围.
的取值范围.(1)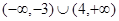 ;(2)
;(2)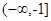
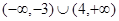 ;(2)
;(2)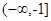
本试题主要考查了绝对值不等式的求解,以及函数的定义域的概念的综合运用。
(1)因为函数 . 当
. 当 时,求函数
时,求函数 的定义域,就是使真数大于零的x的取值范围。
的定义域,就是使真数大于零的x的取值范围。
(2)利用不等式 即
即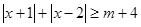
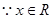 时,恒有
时,恒有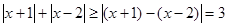 ,
,
所以不等式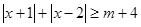 解集是R,
解集是R,
只要m+4小于等于其最小值即可。
解:(1)由题设知: ,
,
不等式的解集是以下不等式组解集的并集:
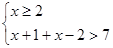 ,或
,或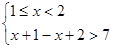 ,或
,或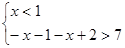
解得函数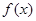 的定义域为
的定义域为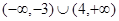 ;
;
(2)不等式 即
即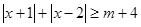 ,
,
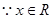 时,恒有
时,恒有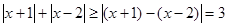 ,
,
不等式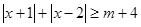 解集是R,
解集是R,
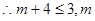 的取值范围是
的取值范围是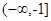
(1)因为函数
 . 当
. 当 时,求函数
时,求函数 的定义域,就是使真数大于零的x的取值范围。
的定义域,就是使真数大于零的x的取值范围。(2)利用不等式
 即
即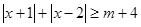
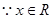 时,恒有
时,恒有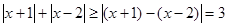 ,
,所以不等式
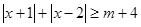 解集是R,
解集是R,只要m+4小于等于其最小值即可。
解:(1)由题设知:
 ,
,不等式的解集是以下不等式组解集的并集:
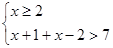 ,或
,或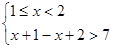 ,或
,或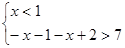
解得函数
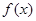 的定义域为
的定义域为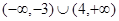 ;
;(2)不等式
 即
即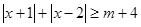 ,
,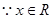 时,恒有
时,恒有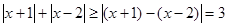 ,
,不等式
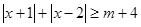 解集是R,
解集是R,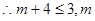 的取值范围是
的取值范围是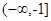

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
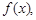 若存在
若存在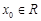 ,使
,使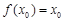 成立,则称点
成立,则称点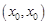 为函数的不动点,对于任意实数
为函数的不动点,对于任意实数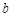 ,函数
,函数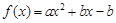 总有相异不动点,实数
总有相异不动点,实数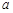 的取值范围是____
的取值范围是____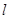 与函数
与函数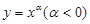 的图象切于点
的图象切于点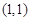 ,则直线
,则直线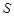 的取值范围为( )
的取值范围为( )



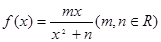 在
在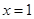 处取到极值
处取到极值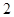
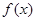 的解析式;
的解析式;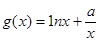 ,若对任意的
,若对任意的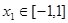 ,总存在
,总存在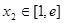 ,使得
,使得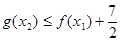 ,求实数
,求实数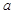 的取值范围.
的取值范围.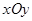 中,
中,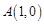 、
、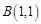 、
、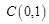 ,映射
,映射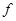 将
将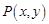 对应到另一个平面直角坐标系
对应到另一个平面直角坐标系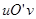 上的点
上的点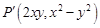 ,则当点
,则当点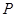 沿着折线
沿着折线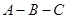 运动时,在映射
运动时,在映射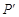 的轨迹是( )
的轨迹是( )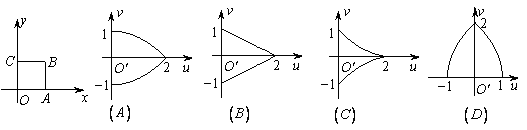
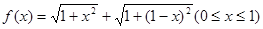 的性质,构造了如下图所示的两个边长为1的正方形
的性质,构造了如下图所示的两个边长为1的正方形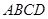 和
和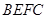 ,点
,点 是边
是边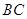 上的一个动点,设
上的一个动点,设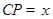 ,则
,则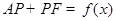 . 请你参考这些信息,推知函数
. 请你参考这些信息,推知函数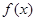 的图象的对称轴是 .
的图象的对称轴是 . 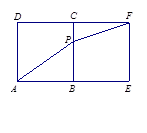
 ,若存在开区间
,若存在开区间 和常数C,使得对任意的
和常数C,使得对任意的 都有
都有 ,且对任意的x
,且对任意的x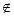 (a,b)都有
(a,b)都有 恒成立,则称函数
恒成立,则称函数 是R上的“Z型”函数;
是R上的“Z型”函数; 对任意的x
对任意的x R恒成立,求实数t的取值范围.
R恒成立,求实数t的取值范围.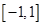 上存在零点,求实数p的取值范围;
上存在零点,求实数p的取值范围; 的值域为区间
的值域为区间 ,且
,且