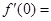题目内容
对定义在区间l,上的函数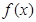 ,若存在开区间
,若存在开区间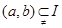 和常数C,使得对任意的
和常数C,使得对任意的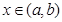 都有
都有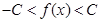 ,且对任意的x
,且对任意的x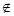 (a,b)都有
(a,b)都有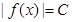 恒成立,则称函数
恒成立,则称函数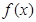 为区间I上的“Z型”函数.
为区间I上的“Z型”函数.
(I)求证:函数 是R上的“Z型”函数;
是R上的“Z型”函数;
(Ⅱ)设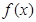 是(I)中的“Z型”函数,若不等式
是(I)中的“Z型”函数,若不等式 对任意的x
对任意的x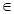 R恒成立,求实数t的取值范围.
R恒成立,求实数t的取值范围.
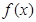 ,若存在开区间
,若存在开区间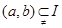 和常数C,使得对任意的
和常数C,使得对任意的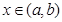 都有
都有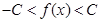 ,且对任意的x
,且对任意的x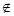 (a,b)都有
(a,b)都有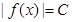 恒成立,则称函数
恒成立,则称函数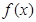 为区间I上的“Z型”函数.
为区间I上的“Z型”函数.(I)求证:函数
 是R上的“Z型”函数;
是R上的“Z型”函数;(Ⅱ)设
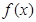 是(I)中的“Z型”函数,若不等式
是(I)中的“Z型”函数,若不等式 对任意的x
对任意的x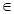 R恒成立,求实数t的取值范围.
R恒成立,求实数t的取值范围.(Ⅰ)函数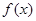 为
为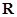 上的“
上的“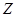 型”函数. (Ⅱ)
型”函数. (Ⅱ)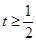 或
或 .
.
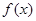 为
为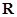 上的“
上的“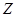 型”函数. (Ⅱ)
型”函数. (Ⅱ)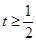 或
或 .
.本试题主要是考查了绝对值不等式和绝对值函数的运用。
(1)因为根据新定义可知,函数 是否是R上的“Z型”函数,只要判定。对任意的
是否是R上的“Z型”函数,只要判定。对任意的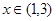 都有
都有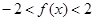 ,且对任意的
,且对任意的 都有
都有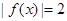 恒成立即可
恒成立即可
(2)不等式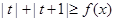 对一切的
对一切的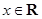 恒成立,只要
恒成立,只要 即可这样可知得到t的取值范围。
即可这样可知得到t的取值范围。
(1)因为根据新定义可知,函数
 是否是R上的“Z型”函数,只要判定。对任意的
是否是R上的“Z型”函数,只要判定。对任意的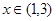 都有
都有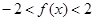 ,且对任意的
,且对任意的 都有
都有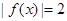 恒成立即可
恒成立即可(2)不等式
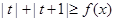 对一切的
对一切的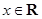 恒成立,只要
恒成立,只要 即可这样可知得到t的取值范围。
即可这样可知得到t的取值范围。
练习册系列答案
相关题目
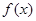 的导数为
的导数为 ,且
,且 时,
时,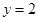 ,则这个函数的解析
,则这个函数的解析 
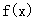 在区间
在区间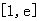 上的最大值和最小值,(
上的最大值和最小值,(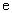 是自然对数的底数),
是自然对数的底数),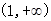 上,函数
上,函数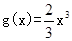 的图像的下方。
的图像的下方。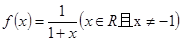
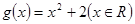
 和
和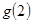 的值
的值 (2)
(2) 的值,并求
的值,并求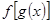 的解析式。
的解析式。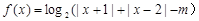 .
. 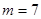 时,求函数
时,求函数 的定义域;
的定义域;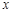 的不等式
的不等式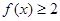 的解集是
的解集是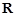 ,求
,求 的取值范围.
的取值范围. .
. 在
在 上是增函数,求正实数
上是增函数,求正实数 的取值范围;
的取值范围;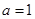 ,
, 且
且 ,设
,设 ,求函数
,求函数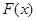 在
在 上的最大值和最小值。
上的最大值和最小值。 在
在 处取得极值,则
处取得极值,则 的值为()
的值为()  +
+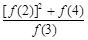 +
+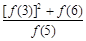 +
+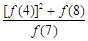 +
+ 的值为_______________.
的值为_______________. ,则
,则